Résumé : pour imprimer un papier peint que l’on pose habituellement sur les murs, on se sert d’un cylindre sur lequel est gravé un motif de base. La rotation du cylindre reproduit infiniment le même motif. Similairement, l’ordinateur peut reproduire des motifs riches modulés par de subtiles variations pour donner ce que Alexandre Dewdney appelle papier peint cérébral.
Mots-clés : itération, cercle, convergence, symétrie.
L’exercice s’inspire de l’article intitulé Récréation informatique : l’ordinateur fabrique des papiers peints cérébraux dont les motifs sont presque, mais pas tout à fait répétitifs, par A. Dewdney, Pour la science, novembre 1988.
Pour imprimer le papier peint que l’on pose habituellement sur les murs, on se sert d’un cylindre sur lequel est gravé un motif de base. La rotation du cylindre reproduit indéfiniment le même motif. Similairement, l’ordinateur peut reproduire des motifs riches modulés par de subtiles variations pour donner ce que l’on appelle un papier peint cérébral. Ces motifs ne se répètent pas à l’identique. Que l’on se déplace de droite à gauche ou de haut en bas, aussi bien la forme du motif que son environnement varient continuellement. Alors, d’un emplacement à l’autre, qu’est-ce qui change et qu’est-ce qui se conserve ?
On considérera dans cet exercice, trois exemples de papiers peints cérébraux. Ils sont particulièrement simples à mettre en oeuvre avec un ordinateur. Le premier a été imaginé par John Connet, Barry Martin et Tony Smith. Ce programme est baptisé cercle et, pourtant, reproduit des formes qui ressemblent plus à des carrés. L’explication réside dans le fait que l’expression utilisée pour fabriquer le papier peint part de la construction d’un cercle, x2 + y2, qui affecte une couleur au point de coordonnéesx,y. Le programme est en fait assez simple. Il suffit de choisir un point de coordonnées x,y de calculer l’expression correspondante aux coordonnées sur le cercle de ce point, c’est-à- dire en calculant x2 + y2 et de considérer la partie entière de cette valeur. Le point x,y est noir lorsque la partie entière est paire et il est blanc lorsque la partie entière est impaire. C’est aussi simple que cela. On peut rajouter un petit peu de complexité en considérant des restes de division par d’autres valeurs et en prenant des couleurs différentes pour chacun de ces restes.
Il est conseillé de considérer une zone rectangulaire et de parcourir tous les points de cette zone et d’effectuer la boucle pour calculer la couleur de chacun de ces points.
Le deuxième exemple a été imaginé par Barry Martin. Il part sur le même principe que l’exemple ci-dessus, mais utilise des formules un peu différentes pour calculer à chaque itération une nouvelle valeur pour x ou pour y dépendant l’une de l’autre. Il suggère, par exemple, l’emploi du couple de formules ci-dessous qui peut engendrer des images étourdissantes.
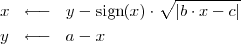
La fonction sign(x) prend la valeur 1 ou -1, selon que x est positif ou négatif.
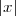représente la valeur absolue de x. L’algorithme pour résoudre de problème est
très simple, on peut le perfectionner en y incorporant, par exemple, un moyen de
déplacer les points qui tombent en dehors des limites de l’écran, ou de
comprimer les parties extérieures du dessin pour les ramener dans la zone
visible.
Considérant ce même exemple, on pourra également prendre le couple de formules d’itération suivant :
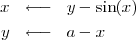
Le troisième exemple de papier peint cérébral est formé de motifs qui vont des volutes persanes aux exubérances incas. Les algorithmes de ces créations diffèrent de ceux mentionnés plus haut. Ce sont en fait des variantes de l’automate cellulaire autoreproducteur, inventé par Edward Fredkin du MIT en 1960.
L’automate cellulaire de Fredkin consiste à imaginer, sur un plan, un quadrillage illimité formé d’un infinité de cellules carrées. A chaque instant, toute cellule ne peut posséder que l’un des deux états. Elle peut être, par exemple, vivante ou morte et il y a quelque part une horloge qui rythme le temps. L’état suivant de chaque cellule est déterminé par l’état présent des quatre cellules adjacentes.
Si, parmi ces quatre cellules, le nombre des vivantes est pair, la cellule de base sera morte au cycle suivant, quel que soit son état actuel. Inversement, elle revivra au cycle suivant si elle possède un nombre impair de voisines vivantes. Cette règle est appliquée simultanément à toutes les cellules du plan. Cet automate ressemble, bien évidemment, beaucoup au jeu de la vie inventé par John Horton Conway et dont on entend parler très souvent. Il faut noter toutefois que l’automate de Fredkin a été inventé avant celui de Conway et qu’il est beaucoup plus simple.
Cet automate possède en outre une propriété surprenante que ne possède pas le jeu de la vie, toute configuration initiale de cellule vivante se développe pour redonner quatre configurations identiques, après un certain nombre de générations. Après quelques générations de plus, on obtient donc seize copies du motif initial, puis soixante-quatre et ainsi de suite. On observe les plus beaux effets décoratifs pendant les phases intermédiaires entre celles qui reproduisent le motif initial.
Le problème consiste donc à écrire un programme permettant de reproduire des papiers peints comme ceux décrits, voire en inventer de nouveaux.
Pour le premier exemple, on peut considérer qu’il suffit de donner les coordonnées A et B de l’angle inférieur gauche du carré à explorer, puis la longueur du côté de ce carré. On pourra, par exemple, fournir comme valeur A = -15, B = -20 et comme côté 87. Le programme va donc explorer un quadrillage de 100 par 100 dans un carré de 87 unités de côté, situé au-dessus et à droite du point (-15,-20).
Pour le deuxième exemple, on peut considérer les constantes suivantes : A = -200, B = 0.1 et C = -20. Autre valeurs conseillées : A = 0.4, B = 0.1, C = 0 ; ou encore : A = -3.14, B = 0.3 et C = 0.3.
Pour les valeurs A = -1000, B = 0.1 et C = -10, on obtient une forme d’écorce de citron quadrangulaire. Bien entendu le nombre d’itérations est fondamental. Plus le nombre d’itérations est élevé, mais là il faudra compter beaucoup de temps pour l’exécution, plus le dessin sera de qualité.
Pour la deuxième partie de l’exemple 2, le seul paramètre à spécifier est le paramètre A. On peut obtenir des dessins particulièrement intéressants en prenant des valeurs de A situées à moins de 0.07 du nombre π.
Pour le troisième exemple, il est conseillé de donner au départ un motif initial, puis de calculer l’algorithme de Fredkin et, pour chaque voisin de la cellule de base, si la cellule voisine est vivante, on l’additionne, on calcule la parité et, selon la parité, la cellule sera vivante ou morte à la génération suivante.
La solution actuellement proposée est donnée par les fichiers MatLab : cercle.m, hopalong.m et friedkin.m.