Résumé : changer l’échelle du temps, c’est possible avec un ordinateur. Simuler le déplacement des étoiles est un exercice courant en informatique. Le problème est —théoriquement— relativement simple : il suffit de se référer aux lois de la gravitation. Il faudra malgré tout prendre garde à l’interprétation du résultat : la moindre erreur peut provoquer un comportement chaotique !
Mots-clés : simulation, gravitation, force, trajectoire, vitesse, accélération.
L’exercice s’inspire de l’article Récréations informatiques, La simulation des amas d’étoiles de A. Dewdney, Pour la Science, Mars 1986.
”Dans toutes les régions de l’Univers, c’est un merveilleux ballet cosmique que la gravitation fait danser aux amas d’étoiles. A l’échelle d’une vie humaine, chaque étoile se déplace de façon imperceptible, mais si on change l’échelle du temps afin qu’une année corresponde à une seconde, les orbites des étoiles s’entrecroisent et forment un écheveau très complexe. Parfois une étoile passe très près d’une étoile voisine et amorce avec elle un pas de deux qui la projette au loin dans l’espace. Quand ces événements deviennent fréquents, l’amas se désagrège et son noyau finit par disparaître.
Si un télescope puissant est capable de révéler la structure de quelques-uns des amas d’étoiles qui peuplent notre Galaxie, il lui est impossible de changer l’échelle du temps et ramener les années à quelques secondes ; seul un ordinateur peut accomplir ce miracle. En fait, on peut substituer l’ordinateur au télescope pour observer l’évolution d’amas d’étoiles fictifs : une succession d’instantanés indique le mouvement de chacun des astres.
Les forces de gravitation sont-elles seules responsables de l’évolution des amas d’étoiles ? (...) De nombreux théoriciens et experts en simulation ont confronté les résultats des simulations avec les observations effectuées sur les amas réels.
Il n’est pas difficile d’écrire la chorégraphie d’un ballet cosmique, car les interactions stellaires découlent de la loi classique de la gravitation : chaque étoile exerce sur chaque autre étoile une force d’attraction proportionnelle au produit des masses et inversement proportionnelle au carré de la distance séparant les deux étoiles. Ces forces d’attraction sont donc faciles à calculer et les mouvements qui se produisent au sein d’un amas ne sont que le résultat de leur action simultanée.
(...) Vers le centre de l’amas, on observe des trajectoires aux oscillations erratiques ; à la périphérie, les étoiles ont tendance à s’éloigner, puis à s’arrêter et à revenir. Lorsque deux étoiles passent très près l’une de l’autre, elles exercent l’une sur l’autre une force gravitationnelle qui augment en modifiant notablement leur trajectoire. Des évasions hors de l’amas proviennent généralement d’un ou plusieurs croisements rapprochés de ce type. Quant une étoile d’écarte de son amas d’origine, elle finit par revenir au bien elle s’échappe à jamais. Tout objet astronomique possède une vitesse de libération qui dépend de sa masse et de celle de l’astre ou du système dont il s’échappe. Si une étoile s’éloigne d’un amas à une vitesse supérieure à sa vitesse de libération, elle ne reviendra jamais. Les néophytes de la simulation observent souvent des évasions hors de l’amas qu’ils ont défini. Il n’est pas rare au début de voir se désintégrer dès les premiers instants le ballet que l’on espérait contempler : mieux vaut donc commencer par construire des systèmes de deux ou trois étoiles.”
Le programme doit permettre de simuler des amas d’étoiles fictifs, voire des amas réels (prendre les étoiles les plus rapprochées du soleil).
Le programme est composé de plusieurs boucles permettant de calculer à chaque instant t l’accélération en x, y et z. Puis on calcule la vitesse et finalement la position. Les informations minimales à donner pour chaque étoiles sont : la position initiale, la vitesse initiale, le nom, la masse et la couleur.
Le tableau ci-dessous donne les informations sur les étoiles les plus proches du Système solaire :
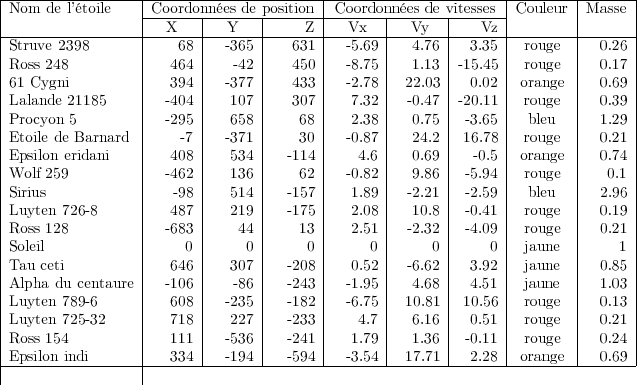
La solution actuellement proposée est donnée par les fichiers MatLab : amas.m et AmasDef.m.