Résumé : nombreux sont les utilisateurs du ballon rond qui ne savent pas comment il est arrangé. On peut formuler la question différemment : comment décomposer une surface de sphère en hexagones et pentagones ? La solution est étonnante. Elle permet de redécouvrir des notions intéressantes d’algèbre linéaire et de géométrie.
Mots-clés : algèbre, géométrie, espace, formule d’Euler, polyèdre, matrice, trigonométrie sphérique, fullerène, radiolaire, icosaèdre, dodécaèdre.
L’exercice s’inspire de l’actualité : en juin 1998 à Paris le Mondial bat son plein et de nombreux fans de football ne savent même pas comment un ballon est fabriqué : certains ont malgré tout aperçu des pentagones et des hexagones (les couleurs noires et blanches peuvent les aider). En regardant d’un peu plus près on constate des symétries intéressantes, certaines régularités...
Le ballon de football peut être observé comme un objet mathématique très intéressant : un polyèdre. On peut poser le problème de la façon suivante : comment décomposer une surface de sphère en hexagones et pentagones réguliers ?
Sans donner trop rapidement la solution, le problème permet de (re-) découvrir le dodécaèdre, l’icosaèdre tronqué et autres polyèdres. On peut également expliquer pourquoi les radiolaires ont des squelettes qui ne peuvent être constitués uniquement d’hexagones. En plaçant des atomes de carbones sur les sommets d’un ballon de football, on peut créer une molécule appelée fullerène ou C60 (carbone-60).
Le problème consiste donc à représenter un ballon de football ou fullerène ou icosaèdre tronqué (puisque tous ces objets sont les mêmes).
Craignant que les supporters de football soient plus intéressés par les matchs que par la résolution du problème, les indications seront nombreuses.
On peut commencer par définir un polyèdre (de la même façon que l’on définit un polygone) : un polyèdre est un ensemble de figures planes délimitant une portion de l’espace. Tous les termes utilisés sont issus de la Grèce antique. Platon, le fameux philosophe grec, laissa l’empreinte de sa pensée dans les Eléments d’Euclide. Cet ouvrage, resté pendant des siècles le seul livre de géométrie, s’intéressait aux droites et figures idéales. Les droites idéales sont droites et les polygones idéaux sont réguliers, c’est-à-dire, ont tous les côtés et tous les angles égaux. Le polygone le plus simple est le triangle équilatéral. C’est le plus simple car il dispose du plus petit nombre de côtés possible pour délimiter une portion du plan. Il est intéressant de constater que les Eléments d’Euclide débutent par une proposition décrivant un triangle équilatéral et se termine par une étude sur les cinq solides réguliers. Chacun de ceux-ci ont des polygones réguliers sur toutes les faces. Ils sont connus aujourd’hui comme les cinq solides platoniciens. Le tétraèdre dispose de quatre faces formées de triangles équilatéraux. C’est le polyèdre le plus simple puisqu’il dispose du plus petit nombre possible de faces délimitant une portion de l’espace.
Avec le triangle équilatéral, les polygones suivants peuvent être décrits : le carré (quatre côtés), le pentagone (cinq côtés), l’hexagone (six côtés), l’octogone (huit côtés), l’ennéagone (neuf côtés), le décagone, etc.
On retrouve les polygones réguliers dans les polyèdres réguliers. Seulement trois sont utilisés : l’hexaèdre appelé communément cube (six faces) est composé uniquement de carrés ; l’octaèdre (huit faces) contient des triangles équilatéraux ; le dodécaèdre (12 faces) est formé de pentagones et finalement, l’icosaèdre a vingt faces qui sont des triangles équilatéraux. Les Eléments d’Euclide se terminent par une démonstration qu’il n’y a que cinq polyèdres réguliers.
Sans donner une démonstration formelle, on peut constater que (de la même façon que deux côtés se rejoignent en un point) deux faces se rejoignent en une droite (arête) ; donc chaque face partage une arête avec une autre face ou une arête appartient exactement à deux faces (et pas plus). Les arêtes se rejoignent en un point appelé sommet du polyèdre.
Dans un tétraèdre, trois arêtes se rencontrent en un sommet ou chaque sommet est entouré de trois triangles. Il est intéressant de disposer ces trois triangles à plat et de noter la somme des angles en un sommet. Trois fois soixante degrés donne 180∘. Si l’on ajoute un triangle, on a alors 240∘, mais on dispose alors d’un octaèdre. En introduisant un cinquième, on trouve 300∘ ; il s’agit alors de l’icosaèdre. Un sixième triangle donnerait une somme de 360∘ et l’on voit immédiatement qu’aucun sommet de polyèdre ne peut exister car tout est plat. On peut ensuite essayer avec les carrés. Un minimum de trois est nécessaire, 3 × 90∘ = 270∘ et l’on obtient un sommet de cube. Un quatrième carré donnerait un total de 360∘ et à nouveau, tout est à plat. Avec des pentagones, un minimum de trois faces donne le dodécaèdre (avec quatre on dépasse 360∘. Avec des hexagones, un minimum de trois est déjà trop (3 × 120∘ = 360∘). Et de la même façon pour les polygones avec plus de côtés. De la sorte, on peut observer qu’il n’y a que cinq polyèdres réguliers.
On peut aborder le problème par l’algèbre linéaire. On prend : x, le nombre pentagones, y, le nombre d’hexagones, f, le nombre de faces, a, le nombre d’arêtes et s, le nombre de sommets ; ces nombres sont des entiers positifs. Alors on a les équations suivantes :
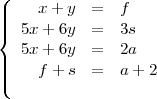
La première équation indique que le nombre de faces est égal au nombre de pentagones plus le nombre d’hexagones. La deuxième équation est le résultat du constat : chaque sommet sépare trois faces ou chaque sommet est compté trois fois puisqu’il appartient à trois faces différentes (chaque pentagone a cinq sommets, chaque hexagone a six sommets, le nombre total de sommets des polygones est trois fois celui de la sphère). La troisième équation est le résultat d’un raisonnement similaire sur les arêtes : le nombre total d’arêtes définis par les pentagones et les hexagones est compté deux fois puisque chaque arête sépare deux faces. La dernière équation est donnée par la relation d’Euler qui s’énonce comme suit : dans tout polyèdre, le nombre d’arêtes augmenté de 2 est égal au nombre de faces augmenté de celui des sommets.
La résolution du problème débute donc par la résolution des quatre équations à cinq inconnues. Une méthode simple consiste à permuter les lignes et à les additionner afin de ne conserver que des uns dans la diagonale et des zéros en dessous. Ci-dessous, on trouvera quelques étapes de la résolution :
On réécrit les équations :

On prend la ligne 2 et on lui soustrait deux fois la ligne 1 :

On permute la ligne 3 et la ligne 2 :
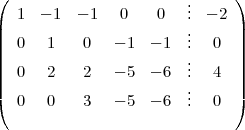
La ligne 3 moins 2 fois la ligne 2 :
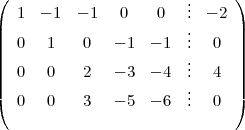
On place un 1 dans la diagonale :
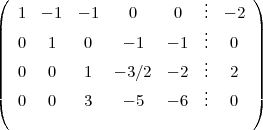
La ligne 4 moins 3 fois la ligne 3 :
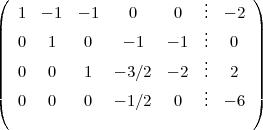
On place un 1 dans la diagonale :
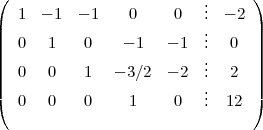
Etonnant : la ligne 4 nous indique que : x = 12. Cela signifie qu’il y a nécessairement 12 pentagones (x est une inconnue principale), le nombre d’hexagones étant libre (y est une inconnue secondaire).
Si y = 0, alors on a un polyèdre régulier très connu : il comporte 12 faces pentagonales régulières. Il s’agit du dodécaèdre, un des cinq polyèdres platoniciens.
Les radiolaires possèdent presque tous un squelette de forme et de structure diverses, souvent très délicat et décoratif contenant toujours de la silice, parfois pure et amorphe. Les structures répondent aux conditions du problème : on peut donc affirmer qu’il est impossible de trouver des radiolaires dont le squelette est constitué uniquement d’hexagones.
Les chimistes ont décrit, puis synthétisé des molécules composées uniquement d’atomes de carbone disposés sur une sphère et formant les sommets de pentagones et d’hexagones, ainsi la molécule C60 qui est la reproduction atomique du ballon de football. Il y a en a d’autres : C32, C50, C60, C70, C240,C540, C960.
Il reste donc à décrire le ballon de football ; pour cela, il faut décrire plus précisément les polyèdres réguliers. Platon découvre qu’il n’y a que cinq polyèdres réguliers convexes pouvant être inscrits dans une sphère.
On peut démontrer par la trigonométrie sphérique que l’angle d’inclinaison de deux faces adjacentes est donné par :
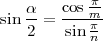
où m est le nombre d’arêtes en un sommet et n est le nombre de côtés de chaque face.
La longueur de l’arête d’un polyèdre régulier se calcule par la formule :
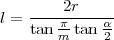
où r est le rayon de la sphère circonscrite.
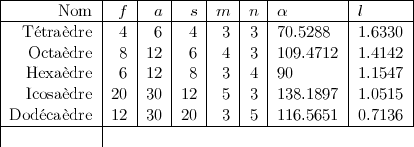
Le tableau ci-dessous décrit les cinq polyèdres réguliers convexes inscrits dans une sphère de rayon 1 :
Pour calculer les coordonnées d’un icosaèdre on place les sommets 6 et 7 le long de l’axe des z comme ci-dessous :
De 6 comme centre, on prend une sphère de rayon l égal à la longueur de l’arête du polyèdre. L’équation du plan d’intersection de cette sphère avec la sphère de rayon 1 circonscrite au polyèdre est donnée par :
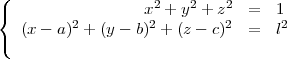
où a, b et c sont les coordonnées du centre de la sphère (ici le sommet 6), donc a = 0, b = 0 et c = 1). On a donc :
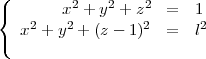
d’où
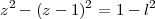
ou encore, le plan P d’intersection est donné par l’équation :
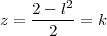
Le plan coupe la sphère unitaire suivant le cercle d’équation :
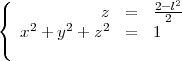
ou encore,
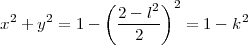
Le rayon du cercle d’intersection est :
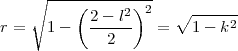
De dessus, on observe alors un cercle de rayon r. En plaçant le sommet 1 sur l’axe des x, on a donc l’image ci-dessous. A droite on retrouve les points situés au-dessous du plan Oxy ; ils peuvent être obtenus par symétrie centrale des sommets «supérieurs».
On obtient ainsi les coordonnées des sommets de l’icosaèdre. Pour passer au ballon de football, il faut alors tronquer cet icosaèdre. Si l’on observe ce qui se passe au sommet 6 : on prend un plan horizontal ; celui-ci coupe l’icosaèdre en cinq points puisqu’il y a cinq faces triangulaires issues du sommet ; on obtient donc un pentagone. Comme il y a douze sommets, en procédant de la même façon, on obtient douze pentagones (on retrouve la solution algébrique). Il nous reste donc douze faces pentagonales et les vingt faces (qui étaient précédemment des triangles) hexagonales. Pour aider le lecteur, l’icosaèdre tronqué avec les numéros des sommets (face avant) sont donnés ci-dessous.
La solution actuellement proposée est donnée par les fichiers MatLab : ballon.m