Chapitre 46
Le jour de la semaine

Résumé : le premier jour de l’an 2000 sera un samedi. Christophe Colomb a découvert l’Amérique un vendredi. Le 29 février de l’an 2000 est un mardi. Il n’y a pas eu de 29 février en 1900. Pour déclarer avec assurance ce type d’information, il faut maîtriser le fonctionnement du calendrier (julien et grégorien). C’est le but de cet exercice.

Mots-clés : calendrier, résidu, reste.

Enoncé

L’exercice s’inspire du livre Récréations arithmétiques de Emile Fourrey, Librairie Vuibert, Paris, 1899.

L’énoncé est en réalité très simple : à quel jour de la semaine correspond une date donnée ? Un bref historique des réformes subies par le calendrier est nécessaire.

L’année tropique contient 365 jours et, 242217 millionièmes de jour, ou encore, 365j,242217. C’est l’année tropique qui règle le retour des saisons, c’est elle qui doit servir de base à l’année civile et au calendrier.

En prenant une année civile qui comprend seulement 365 jours, comme le faisaient les Egyptiens, on commet une erreur qui, au bout d’un certain nombre d’années, peut devenir importante. En 100 ans, les dates avanceraient sur les véritables de

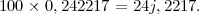
Les Romains conservèrent longtemps cette division de l’année en 365 jours. Mais, au temps de Jules César, les saisons se trouvant complètement déplacées, le dictateur décida que dans une période de 4 années consécutives, les trois premières années renfermeraient 365 jours et la quatrième 366. L’année julienne est donc égale à 365j,1∕4 = 365j,25.

Les évêques, réunis en concile à Nicée, en 325, s’occupèrent entre autres choses, de régler la date de la fête de Pâques d’une façon précise. A cet effet, ils conservèrent le calendrier julien, donnèrent le nom de bissextile à la 4^e année et décidèrent que les années bissextiles seraient celles dont le millésime serait divisible par 4.

Mais l’année julienne étant trop longue de 365j,25 - 365j,242217 = 0j,007783, soit d’environ 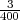, l’équinoxe de printemps arrivait en 1582 le 11 mars (au lieu du 21 mars). Cette année-là, le pape Grégoire XIII supprima 10 jours au calendrier et décida que le lendemain du jeudi 4 octobre serait le vendredi 15 octobre et qu’afin d’éviter le retour de pareil état de choses, on retrancherait au calendrier 3 jours en 400 ans ; pour cela, les seules années séculaires qui resteraient bissextiles seraient celles dont le millésime indique un nombre de siècles divisible par 4. Ainsi, 1600 a été bissextile, 1700, 1800 et 1900 ne l’ont pas été, mais 2000 le sera.

L’expression

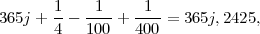
qui donne la valeur de l’année grégorienne, fait voir en même temps les réformes successives subies par le calendrier.

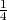• + indique que tous les 4 ans, on ajoute un jour à l’année ;
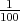• -, que tous les 100 ans on retranche un jour à chaque centième année qui devrait être bissextile ;
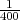• +, que tous les 400 ans, on reprend l’année bissextile.

Le calendrier grégorien laisse bien encore subsister une légère erreur, mais elle n’est que d’environ 1 jour en 4000 ans. On peut donc admettre, sans erreur sensible, que la durée de l’année est celle indiquée par le calendrier grégorien, soit 365j2425.

En effectuant sa réforme, le pape Grégoire XIII avait surtout pour but de replacer la fête de Pâques à l’époque fixée par le concile de Nicée. Il rétablit donc la date du 15 octobre 1582 en supposant exactes les dates de l’année 325. Or elles ne l’étaient pas, car les années 100, 200, 300 n’auraient pas dû être bissextiles. Il a donc dû s’écouler entre les années 1 et 325 un nombre de jours plus grand que celui indiqué par le calendrier grégorien actuel, dont le point de départ, au lieu d’être comme on pourrait le croire, à l’an 1 de notre ère, est en réalité l’année 325.

En effet, les 324 années comprises entre le commencement de notre ère et l’an 325 ont contenu

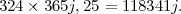
Si le calendrier grégorien avait été appliqué à partir de l’an 1, elles n’auraient contenu que

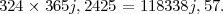
Soit une différence de 2j,43. Ainsi, il s’est écoulé réellement 2j43 de plus que le calendrier grégorien n’en compte depuis le commencement de notre ère, c’est-à-dire que toutes les dates — par rapport aux jours de la semaine — devraient être avancées en conséquence. Par exemple, le dimanche 1^er janvier 1899 aurait dû s’appeler 3 janvier.

Depuis le commencement de notre ère, les jours de la semaine se sont succédé sans interruption dans leur ordre naturel. Lors de la réforme grégorienne, seuls les quantièmes furent modifiés : le lendemain du jeudi 4 octobre 1582 fut le vendredi 15 octobre.

Les Russes et les grecs ont conservé le calendrier julien. Pour les autres nations européennes, le calendrier julien doit être appliqué, en général, depuis l’an 1 jusqu’au 4 octobre 1582 inclusivement et le calendrier grégorien, à partir du 15 octobre 1582.

Le but du problème consiste à chercher le jour de la semaine, quelle que soit la date, et à construire, par la même occasion, un calendrier perpétuel.

Indications

Emile Fourrey donne de précieuses indications qui permettront de résoudre aisément ce problème :

• lorsqu’on retranche ou qu’on ajoute à une date un nombre de jours multiple de 7, on tombe sur le même jour de la semaine que celui de la date considérée ;
• dans le calcul du jour de la semaine correspondant à une date, connaissant le jour relatif à une date déterminée, on pourra négliger les multiples de 7 en ne tenir compte que du reste de la division par 7 du nombre de jours compris entre les deux dates considérées ;
• une année renfermant 52 semaines plus 1 jour ou plus 2 jours, suivant qu’elle n’est pas ou qu’elle est bissextile, le résidu bissextile est, selon le cas, 1 ou 2 ;
• on désignera par partie séculaire du millésime d’une année déterminée la partie de ce millésime qui indique le siècle et par partie annuelle le reste du millésime (ainsi pour l’année 1998, 19 est la partie séculaire et 98, la partie annuelle) ;
• pour trouver à quel jour de la semaine correspond une date quelconque du calendrier julien, on cherchera le résidu (reste de la division par 7) de l’expression obtenue en faisant la somme : 1^o du sextuple de la partie séculaire du millésime de l’année considérée ; 2^o de la partie annuelle ; 3^o du quotient entier de cette partie annuelle par 4 ; 4^o du résidu du premier du mois donné relatif au 1^er mars (tableau ci-dessous) ; et 5^o du quantième donné. Le résidu ainsi obtenu ou numéro sera l’un des nombres 0,1,…,6, désignant respectivement le dimanche, le lundi, ..., le samedi ;
• pour trouver à quel jour de la semaine correspond une date quelconque du calendrier grégorien, on cherchera le résidu (reste de la division par 7) de l’expression obtenue en faisant la somme : 1^o du quintuple de la partie séculaire du millésime de l’année considérée ; 2^o du quotient entier par 4 de cette partie séculaire ; 3^o de la partie annuelle ; 4^o du quotient entier par 4 de cette partie annuelle ; 5^o du résidu du 1^er du mois donné relatif au 1^er mars (tableau ci-dessous) ; 6^o du quantième donné ; et 7^o de 2 unités. Le résidu ainsi obtenu ou numéro sera l’un des nombres 0,1,…,6, désignant respectivement le dimanche, le lundi,... , le samedi ;
• le résidu d’une somme est le même que le résidu de la somme des restes de la division par 7 de chacune des parties composant la somme.

Afin de réduire au maximum les calculs et les chances d’erreurs, quelques règles simples dûes à l’astronome français Delambre (un des inventeurs du système métrique) méritent d’être signalées :

• le n^o d’un quantième est égal au n^o du 1^er du mois, plus le résidu correspondant du quantième diminué de 1 ;
• le n^o d’un quantième d’un mois quelconque s’obtiendra en ajoutant au n^o du jour de la semaine relatif au 1^er mars le résidu du tableau correspondant au quantième diminué de 1.

Le tableau est le suivant :

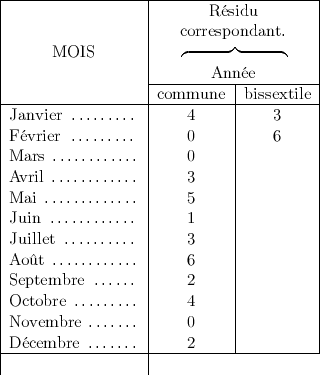
C’est de cette façon que l’on peut démontrer les règles permettant de déterminer le jour dans les calendriers grégorien et julien, ainsi que de construire le calendrier perpétuel.

Solutions

Les solutions sont en cours de développement... Toute solution est la bienvenue.