Résumé : La recherche des nombres premiers et leur répartition sont des thèmes qui fascinent les mathématiciens et font travailler les ordinateurs. Les représentations graphiques des nombres premiers sont difficiles à imaginer. Toutefois, sur la base des travaux de Stanislaw Marcin Ulam, on peut représenter les nombres de diviseurs des nombres entiers et, ainsi, la répartition des nombres premiers.
Mots-clés : nombre premier, diviseur, Riemann, conjecture.
L’exercice s’inspire de l’article Les chasseurs de nombres premiers de Jean-Paul Delahaye, Pour la science, avril 1999.
Il y a plus de deux mille ans, on a identifié les nombres premiers qui ne sont multiples que de 1 et d’eux-mêmes (par exemple : 2, 3, 5, 7, 11, 13, 17, etc.). Ces nombres sont les composants de tous les nombres puisque tout nombre entier peut être décomposé de façon unique en un produit de facteurs premiers (par exemple : 30030 = 2 × 3 × 5 × 7 × 11 × 13).
On a également montré qu’il y a une infinité de nombres premiers. Les chercheurs sont obsessionnellement attachés à la répartition des nombres premiers : quelle est la proportion moyenne des nombres premiers parmi les nombres inférieurs à n ?
Riemann a émis un conjecture pour déterminer cette répartition mais, celle-ci n’a encore jamais été démontrée. De nombreux problèmes et défis autour des nombres premiers excitent encore la curiosités des amateurs.
Stanislaw Marcin Ulam (1909, Lvov Ukraine, 1984, Santa Fe, USA) a résolu le problème de la fusion de la bombe à hydrogène. Il a également utilisé la méthode de Monte-Carlo pour la résolution de problèmes mathématiques. De ses travaux, on a également retenu la spirale d’Ulam : on place tous les nombres entiers le long d’une spirale carrée avec des cercles dont le diamètre est proportionnel au nombre de diviseurs.
Un ordinateur permet de réaliser simplement une représentation de la spirale d’Ulam avec des sphères dont les diamètres sont proportionnels au nombre de diviseurs.
Pour représenter une spirale carrée, on peut observer que les nombres entiers successifs sont à une distance 1 deux fois, puis à une distance 2 deux fois, une distance 3 deux fois, ..., une distance n deux fois. A chaque étape (double) on tourne à gauche.
Pour la représentation à trois dimensions, on représente des sphères à chaque coordonnée des nombres sur la spirale.
Pour définir une sphère, il peut être utile de rappeler que les coordonnées sont données par :
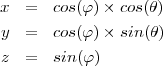
La solution actuellement proposée est donnée par les fichiers MatLab : ulam.m et DemoUlam.m.