Résumé : Le GPS (Global Positioning System) est très répandu. Beaucoup savent l’utiliser mais, peu savent comment le système fonctionne. Les aspects mathématiques du GPS sont expliqués de façon simple ; ils permettent de saisir les principes de la navigation à l’aide des satellites
Mots-clés : GPS, trigonométrie, satellite, équation.
L’exercice s’inspire de l’article Global Positioning System : The Mathematics of GPS Receivers de Richard B. Thompson, Mathematics Magazine, Vol. 71, No 4, 1998.
La navigation par satellite utilise le Global Positioning System (GPS). Ce système, commandé par le Département américain de la défense, a été développé dans les années 80 et est devenu complètement opérationnel en 1995. Le système utilise une constellation de satellites transmettant des fréquences radio, 1227.60mHz et 1575.42mHz.
Au départ, il y avait dix-huit satellites, avec trois satellites dans chacune des six orbites. Actuellement, il y a quatre satellites dans chaque orbite. Les six orbites sont espacées de 60∘ autour de la terre dans des plans inclinés à 55∘ par rapport à l’équateur.
Les orbites sont circulaires à une altitude de 20200km au-dessus de la surface terrestre, avec des périodes de rotation de douze heures. Dans le schéma ci-dessous, on se rend compte que nous vivons entourés d’une cage de satellites en orbite, dont plusieurs sont visibles depuis n’importe quel endroit de la surface de la terre à n’importe quel moment.
On peut placer un récepteur à n’importe quel point de la surface de la terre et, en quelques minutes, il est capable d’indiquer la latitude, la longitude et l’altitude. L’outil offre actuellement une précision de 100m de rayon (sur un plan tangent à la terre) et calcule l’altitude avec une erreur de moins de 160m.
Comment un petit récepteur écoute des satellites et calcule ensuite sa position avec une grande précision ?
On commence en notant exactement le type d’information reçue des satellites. Chaque satellite envoie des signaux, sur les deux fréquences, donnant (i) sa position et (ii) le temps exact de l’envoi.
Le récepteur enregistre la différence Δt entre le temps d’émission et de réception. Si la terre n’avait pas d’atmosphère, le récepteur pourrait utiliser la vitesse C, des ondes radio dans le vide, pour calculer la distance d = CΔt. Cette information suffirait à savoir où l’on se trouve sur une sphère de rayon d centrée au satellite ; malheureusement la couche de gaz qui entoure la terre ralentit les ondes radio et introduit des distorsions dans les mesures de la distance. On corrige partiellement cette erreur en tenant compte de la densité moyenne et de l’épaisseur de l’atmosphère. Les informations de plusieurs satellites sont combinées pour déterminer les coordonnées, latitude, longitude et altitude.
Plusieurs facteurs interviennent dans la précision :
Le but de l’exercice consiste à simuler le fonctionnement du GPS à l’aide d’un ordinateur.
Supposons que vous vous trouviez quelque part à l’intérieur d’une place circulaire de rayon r = 100m.
La place est pavée, sauf dans une zone de forme irrégulière qui vous entoure et recouverte de gravier. La distance moyenne de votre position au bord est de 20m.
Des automobiles se déplacent autour de la place sur une route circulaire. Pour calculer votre position, des messagers quittent leurs automobiles sur la route et se dirigent vers vous. Quand le messager arrive, il vous dit où il se trouvait sur la route et quand. Vous avez une montre et savez que tous les messagers se déplacent à la même vitesse (5m∕sec) sur le pavé mais qu’ils ralentissent à 4m∕sec sur le gravier.
Soit un système de coordonnées au centre du cercle, les distances sont mesurées en cm et le temps en 10e de sec. Un point sur la route est décrit par l’angle depuis le Nord dans le sens des aiguilles d’une montre.
A midi, un messager quitte sa position à 45∘ depuis le Nord. Quand il arrive votre montre indique qu’il est 20.2sec après midi. Comme vous ne pouvez pas savoir la distance exacte parcourue sur le gravier, on prend la distance moyenne de 20m.
A 4m∕sec cela prend 5sec. Pour les 15.2sec restantes, il s’est déplacé sur les pavés couvrant 5m∕sec × 15.2sec = 76m. Vous êtes donc sur un cercle de rayon 76 + 20 = 96m, centré au point de départ du premier messager (P1).
Un deuxième messager quitte la route au point situé à 135∘ depuis le Nord à 12 : 01pm et se déplace dans votre direction. A son arrivée votre montre indique qu’il a mis 29.5sec depuis son départ. Il a passé 5sec sur le gravier pendant les 20m, vous vous trouvez donc dans cercle de rayon 5m∕sec× 24.5sec + 20m = 122.5m + 20m = 142.5m centré au point de départ du deuxième messager (P2).
Les coordonnées des messagers sont (avec une précision de 1∕10) :
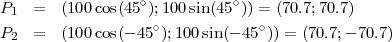
Donc les coordonnées (x0;y0) de votre position satisfont :
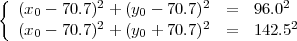
Le système a deux solutions : (-20;39.2) et (161.4;39.2) ; la deuxième se trouve en dehors du cercle. On conclut que vous vous trouvez à 20m à l’Ouest et 39.2m au Nord du centre de la place.
Très bien jusque là. Supposons, pour être prudent, que vous testiez votre position en prenant un troisième messager (à 180∘ depuis le Nord dans votre direction). Il quitte la route à 12 : 02pm et selon votre montre arrive 32.2sec plus tard. Comme précédemment, vous calculez votre distance à P3.
Que s’est-il passé ? Le plus plausible est que votre montre n’est pas synchronisée avec le temps utilisé aux points de départ. Supposons que votre montre fonctionne précisément mais ait une erreur fixe de εsec (où ε < 0 signifie que la montre est en retard).
Si l’on nomme Δt la différence de temps entre le départ et l’arrivée (aperçue sur votre montre), la distance parcourue estimée est :
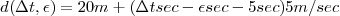
Ainsi le rayon de chaque cercle a une erreur de la même quantité, -5εm. Il doit y avoir une valeur de ε pour laquelle les trois cercles ont un point commun.
Votre montre a une erreur d’approximativement 5sec. L’erreur et les coordonnées de votre position sont donnés par :
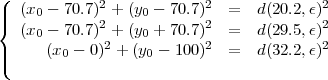
Le système peut être résolu numériquement en prenant des valeurs initiales (par exemple, ε = 0) et des coordonnées estimées pour x0 et y0.
Il n’y a qu’une solution donnant un point à l’intérieur du cercle. En arrondissant à la précision voulue, on a :
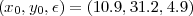
On note vos coordonnées et on jette l’erreur qui ne sert plus. On peut donc utiliser les différences de temps de trois messagers pour déterminer votre position. Les seuls outils nécessaires sont une montre précise mais pas forcément à l’heure et la possibilité de résoudre un système de trois équations à trois inconnues.
Pour comprendre le fonctionnement du GPS dans l’espace, la « place » est maintenant la région délimitée par les satellites, (y compris la Terre), les « automobiles » sont les satellites, les « messagers », les ondes radios et le « gravier », l’atmosphère terrestre. On prend le centre de la Terre comme origine du système de coordonnées. Pour se déplacer à trois dimensions, on a besoin de l’information fournie par quatre satellites S1, S2, S3 et S4.
On suppose que Si est situé à (xi;yi;zi) quand il envoie un signal au temps Ti. Si le signal est reçu au temps Ti′, selon l’horloge du récepteur. On notera Δti = Ti′- Ti et ε représente l’erreur de l’horloge.
Le récepteur calcule d(Δti,ε) qui indique les distances de l’endroit où l’on se trouve à chaque satellite. Notre position (x0;y0;z0) se trouve à l’intersection de quatre grandes sphères. Dans la plupart des cas, il n’y a qu’une valeur possible pour ε qui détermine un unique point.
On résout alors :
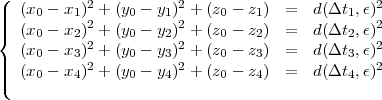
Quand une solution numérique est trouvée, les coordonnées rectangulaires (x0o;y0;z0) sont converties en coordonnées sphériques pour la latitude, la longitude et l’altitude au-dessus de la mer.
En résumé, le récepteur est censé
Une question se pose à propos du GPS : si une personne se tient à un endroit précis et détermine sa position à l’aide d’un récepteur, les coordonnées des positions peuvent changer dans le temps. Comme la position de l’observateur n’a pas changé, les changements sont souvent attribués à la modification des signaux des satellites par le Département américain de la défense. Le Département dégrade occasionnellement les données fournies par les satellites et provoque ainsi une perte de précision pour le GPS. Cette disponibilité sélective (Selective Availability (SA)) devrait disparaître ces prochaines années. Toutefois, la manipulation des signaux n’explique que très peu le changement de position. Le changement est dû avant tout aux erreurs aléatoires dans les mesures, à la sélection des satellites et aux effets de l’atmosphère.
Qu’est-ce qui est fait pour faire disparaître une partie des erreurs aléatoires du positionnement par GPS ? Actuellement, il y a deux méthodes pour améliorer le GPS. Une est le service de positionnement précis (Precise Positioning Service (PPS)), qui est accessible uniquement pour des besoins gouvernementaux. Le système utilise les signaux transmis sur les deux fréquences du GPS pour éliminer la plus grande partie de la variation causée par l’atmosphère terrestre.
Comme pour les différentes couleurs du spectre visible, la réduction de vitesse des ondes radio lorsqu’elles traversent l’atmosphère dépend de la fréquence. De la sorte, des mesures des temps d’arrivée de deux signaux de différentes fréquences peuvent être utilisées pour augmenter considérablement la précision de distances estimées.
La deuxième méthode pour augmenter la précision est utilisée dans les aéroports et les ports. Elle est appelée système de positionnement global différentiel (Differential Global Positioning System (DGPS)). La plus grande partie des erreurs provient des variables aléatoires : atmosphère et satellites. Ainsi, à l’intérieur d’une petite région, l’erreur à chaque instant tend à être indépendante de la position exacte du récepteur. DGPS exploite cette situation en établissant une station de base fixe, dont la position exacte est connue. Un équipement dans cette station de base calcule sa position GPS et la compare à sa position connue ; il envoie continuellement le coefficient de correction. Un récepteur DGPS dans la zone reçoit son information des satellites et calcule sa position. Simultanément, il reçoit la correction courante des sa station de base et l’applique à sa position calculée (on atteint alors une précision de 9 mètres).
La solution actuellement proposée est donnée par les fichiers MatLab : gps.m, gps2d.m et gpserr.m.