Résumé : Quelle est la façon de lacer la plus économique. A l’époque de la globalisation, la question peut préoccuper les gestionnaires mais, les mathématiques peuvent les aider.
Mots-clés : théorème de Pythagore, principe de Fermat, réflexion.
L’exercice s’inspire de l’article Mathématiques sans se lacer ? de Ian Stewart, Pour la science No 224, octobre 1996.
Ian Stewart débute son article par une réflexion sur la fonction du mathématicien : « Qui peut se dire mathématicien ? Il y a quelques années, dans un éclair de rare lucidité, il m’apparut qu’un mathématicien est quelqu’un qui saisit toute opportunité de faire des mathématiques, là où d’autres ne voient pas une possible mathématisation du problème. »
Il existe plusieurs façons de lacer des chaussures : le « zigzag américain », le « collet européen » et l’expéditif « gavage ».
Pour simplifier, on ne considère que les segments rectilignes, la quantité supplémentaire de lacet utilisée pour le nouer étant la même pour toutes les méthodes et pouvant donc être ignorée.
L’ordinateur n’est certainement pas nécessaire pour résoudre ce problème. Il permet toutefois, grâce à une utilisation judicieuse des paramètres et des interfaces graphiques, d’apporter également du plaisir à l’informaticien.
Une attaque frontale du problème consiste à exprimer la longueur du lacet en fonction de trois paramètres :
A l’aide du théorème de Pythagore, il est facile de montrer que les longueurs sont les suivantes :
;
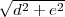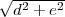+ (n - 2)
;
+ 
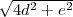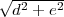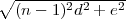.Il est aisé alors de déterminer le laçage le plus court.
On peut considérer le problème sous un autre angle : l’approche géométrique. L’idée est inspirée de l’optique géométrique, l’étude des trajectoires des rayons lumineux.
Une propriété générale des rayons lumineux a été énoncée par Pierre de Fermat : la lumière emprunte le trajet le plus court pour aller d’un point à un autre : on prouve alors que l’angle d’incidence est égal à l’angle de réflexion.
Pour revenir au problème du lacet, on dessine un diagramme de 2n colonnes d’œillets placés verticalement d’une distance d. Deux colonnes successives sont espacées d’une distance e. La dernière colonne représente la colonne d’œillets de gauche, celle d’avant la colonne des œillets de droite, et ainsi de suite alternativement.
Les lignes polygonales zigzaguant au travers du diagramme correspondent aux laçages. Partant de l’œillet du haut à gauche, on dessine le premier segment du laçage en joignant, de droite à gauche, la colonne 1 à la colonne 2, mais le segment suivant sera tracé entre les colonnes 2 et 3 au lieu de revenir de la colonne 2 à la colonne 1, comme sur une véritable chaussure : le segment réel est réfléchi comme si la colonne d’œillets était un miroir. On continuera ensuite de même, chaque segment étant réfléchi dans le miroir-colonne d’où il part. Ainsi le tracé zigzaguant entre deux colonnes d’œillets est remplacé par une ligne progressant toujours vers la gauche.
En considérant que la somme de deux côtés d’un triangle est supérieure au troisième côté, il est facile de déterminer le chemin le plus court.
La solution actuellement proposée est donnée par les fichiers MatLab : lacet.m et demoLacet.m.