Résumé : on connaît le point, le segment de droite, le carré et le cube. Par analogie, on peut imaginer un cube de dimension quatre, l’hypercube. Les ordinateurs sont capables de représenter des projections dans l’espace de l’hypercube.
Mots-clés : dimension, cube, hypercube.
L’exercice s’inspire du livre La quatrième dimension, voyage dans les dimensions supérieures de Thomas Banchoff, Pour la science, Belin, 1996.
Observée au microscope, une amibe (organisme unicellulaire commun dans les eaux dormantes) semble condamnée à une existence à deux dimensions, confinée dans l’étroit espace compris entre la lame et la lamelle. En la regardant de dessus, nous découvrons comment elle se déplace, rencontre d’autres créatures semblables, capture des proies et fuit ses prédateurs. La membrane cellulaire de l’amibe forme une ligne de défense qui l’entoure entièrement et protège son noyau interne des menaces que constituent les autres créatures de la préparation. Toutefois les mots entourer et intérieur ne signifient pas la même chose pour nous, habitants de l’espace à trois dimensions, et pour les habitants de cet espace quasi plat. Aucune amibe de la préparation ne pourrait entrer en contact direct avec le noyau d’une autre. Nous, au contraire, sommes capables d’observer ce micro-organisme de différents points de vue et d’en examiner les parties les plus intimes. Nous pouvons non seulement voir le noyau, mais aussi le toucher, ce qui surprendrait l’amibe et la laisserait perplexe, si elle avait les moyens de l’être. Notre perspective tridimensionnelle nous dévoile des aspects de cet univers microscopique que ne connaîtront jamais ses propres habitants.
Il y a un peu plus de cent ans, un petit livre brillant a exploité cette idée d’interaction entre créatures de dimensions différentes afin d’inciter les lecteurs à se libérer d’une perspective limitée et à envisager de nouvelles manières de percevoir. Son auteur, Edwin Abbott, était pasteur et directeur d’école dans l’Angleterre victorienne.
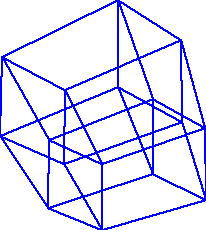
L’analogie est certainement l’idée dominante dans l’histoire de la notion de dimension. Les mathématiciens ont construit des chemins différents pour passer aux dimensions supérieures, créant des suites de figures analogues qui débutaient parfois très bas dans l’échelle des dimensions. Une des suites possibles commence par un point, de dimension zéro et sans aucun degré de liberté. Un point se déplaçant en ligne droite engendre un segment, objet unidimensionnel de base. Un segment se déplaçant perpendiculairement à lui-même dans un plan engendre une figure à quatre sommets, un carré, objet bidimensionnel de base.
Pour continuer dans la troisième dimension, nous déplaçons le carré perpendiculairement à lui-même pour former un cube, objet tridimensionnel de base. L’amibe serait incapable de se représenter cette étape, mais elle pourrait la suivre sur le plan théorique et en déduire certaines propriétés de ce cube impossible à voir, par exemple qu’il possède huit sommets. L’étape suivante consisterait à déplacer le cube dans une quatrième direction perpendiculaire à toutes ses arêtes. Nous obtiendrions un objet quadridimensionnel de base, un hypercube, et bien que nous ne puissions plus visualiser intégralement le processus, nous savons que cette figure présenterait seize sommets.
L’hypercube existe-t-il réellement ? Les mathématiciens estiment qu’ils n’ont pas à répondre à cette question. Ils peuvent déterminer le nombre de sommets et de figures frontalières des équivalents du cube dans n’importe quelle dimension, que ces objets correspondent ou non à une réalité physique.
Pour visualiser les objets et leurs relations au-delà de la troisième dimension, l’instrument idéal est l’ordinateur.
Le but de l’exercice est donc de représenter la projection d’un hypercube sur un écran d’ordinateur et de permettre à l’utilisateur de se déplacer en effectuant des rotations autour de celui-ci.
Il est facile, par analogie, de dénombrer les sommets, les arêtes, les faces et les hyperfaces (qui sont des cubes ordinaires) d’un hypercube. Les sommets sont ceux du cube initial et ceux du cube déplacé, soit 16 en tout. Les sommets homologues des deux cubes sont reliés par une arête, et ces huit arêtes s’ajoutent aux 12 de chacun des deux cubes, ce qui fait en tout 8 + 12 + 12 = 32 arêtes pour l’hypercube. Enfin, on peut montrer que l’hypercube possède 24 faces carrées et huit hyperfaces cubiques.
Les 16 sommets de l’hypercube sont numérotés de 0 à 15 suivant un principe simple : en système de numération binaire, il suffit de quatre chiffres pour écrire ces nombres, soit un chiffre pour chacune des quatre coordonnées du sommet considéré. On code ainsi le sommet no 13 par le nombre binaire 1101 (car 8 + 4 + 0 + 1 = 13) ; avec le quadruplet (1,1,0,1) on obtient presque directement les quatre coordonnées initiales du sommet 13 de l’hypercube.
Après la définition des sommets et des arêtes, il faut effectuer des rotations sur l’hypercube. On détermine entièrement une rotation d’un solide ordinaire à trois dimensions par l’orientation de l’axe de rotation et la valeur de l’angle de rotation ; c’est faux pour un solide à quatre dimensions, car le choix de l’axe de rotation ne suffit pas à caractériser le plan dans lequel la rotation s’effectue : il y a en effet une infinité de directions planes perpendiculaires à une droite donnée. D’autre part, dans l’hyperespace à quatre dimensions comme dans l’espace ordinaire, une rotation d’un solide ne concerne que deux dimensions de ce solide. Lorsqu’on fait tourner un objet à trois dimensions, deux d’entre elles subissent une transformation, tandis que la troisième reste inchangée. Il en va de même pour un objet à quatre dimensions, dont deux sont modifiées et les deux autres inchangées.
Il existe de nombreuses façons de faire tourner un objet à quatre dimensions, mais on peut atteindre chacune des nouvelles configurations par une suite de rotations successives, chacune effectuée dans un plan de coordonnées. Dans l’espace quadridimensionnel, le système de référence comprend quatre axes que l’on peut combiner deux à deux de six façons différentes ; il existe donc six plans de coordonnées. Pour chacun des six plans de coordonnées, il existe une rotation qui peut être définie par une matrice.
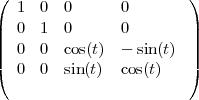
Cette matrice est une matrice de rotation autour du plan XY . Pour trouver les coordonnées de l’hypercube après rotation on multiplie les coordonnées par cette matrice de rotation.
Pour la représentation, on peut projeter l’hypercube dans l’espace ordinaire ou, directement dans le plan. Il suffit dans le premier cas de ne considérer que les trois premières coordonnées et, dans le deuxième cas, les deux premières.
La solution actuellement proposée est donnée par les fichiers MatLab : hypercube.m, hyperDemo.m et hyperDemo.mat.