Résumé : Ligths Out est un jeu fabriqué par Tiger Toys. Il consiste en un tableau contenant 25 lampes/boutons disposés en cinq lignes et cinq colonnes. Au départ certaines lampes sont allumées et d’autres sont éteintes au hasard. Une lampe allumée peut être éteinte en l’enfonçant ; une lampe éteinte peut être allumée en l’enfonçant. Le but du jeu consiste à les éteindre toutes le plus rapidement possible. Les mathématiques peuvent nous aider à résoudre ce problème et même nous donner la solution la plus rapide.
Mots-clés : matrice, linéarité.
L’exercice s’inspire de l’article Two Reflected Analyses of Lights Out de Oscar Martin Sanchez et Cristobal Pareja-Flores, Mathematics Magazine, Vol. 74, Madrid, Spain, No. 4, octobre 2001. Cet article est particulièrement intéressant car il est écrit dans un format utilisant deux colonnes. La colonne de gauche s’adresse à une personne intéressée par une recherche de solution méthodique, la colonne de droite s’adresse au mathématicien. Le lecteur est encouragé à passer d’une colonne à l’autre pour le plaisir et pour mieux comprendre.
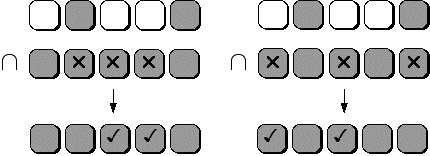
Le jeu Lights out est un puzzle sous forme d’échiquier de dimension cinq sur cinq. Chaque case est formée à la fois d’un bouton et d’une ampoule. Chaque ampoule peut être allumée ou éteinte. En enfonçant le bouton, l’ampoule change d’état ainsi que les ampoules voisines horizontalement et verticalement. Dans l’exemple ci-dessous, les ampoules sont toutes éteintes au départ. Si l’on enfonce les boutons marqués par des croix, on obtient la configuration à droite.
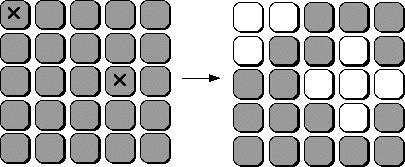
Le but du jeu est, partant d’une configuration initiale aléatoire, d’éteindre toutes les ampoules. Ce jeu peut être généralisé à un échiquier quelconque de dimension m × n.
Comme indiqué plus haut, les auteurs de l’articles ont donné deux solutions. Elle seront décrites ci-après séparément.
Pour résoudre le puzzle, on doit enfoncer un certain nombre de boutons ; pendant ce processus, certaines ampoules sont commutées plusieurs fois mais on n’est intéressé que par le résultat final.
Enfoncer un bouton deux fois de suite n’a pas d’effet. De même résoudre un état donné revient au même que de le résoudre depuis la position complètement éteinte : les mêmes étapes sont nécessaires.
Enfoncer un bouton puis un autre a le même effet que de les enfoncer dans l’ordre inverse. Cela s’explique par le fait que l’état final ne dépend que du nombre de boutons pressés ; il n’a rien a faire avec l’ordre. Ainsi, un ensemble de pressions a le même effet si l’on élimine toutes les paires de pressions identiques. Un tel ensemble de pressions, dans lequel aucun bouton n’est enfoncé plus d’une fois est appelé une procédure.
Le puzzle peut être résolu en essayant toutes les combinaisons possibles. Comme, pour chaque bouton, on peut choisir de l’enfoncer ou non, il y a un nombre colossal de procédures : 225. Il est donc conseillé de trouver une méthode de résolution simplifiée.
Soit une configuration initiale quelconque, si l’on enfonce des boutons de la première ligne alors, pour éteindre les ampoules allumées de cette ligne, la seule solution (sans presser à nouveau un bouton dans la ligne 1 et sans allumer de nouvelles ampoules) est d’enfoncer les boutons qui se situent exactement au-dessous des ampoules allumées de la ligne 1. L’état de la ligne 2 détermine les boutons à enfoncer dans la ligne 3, etc. Ainsi, étant donné un état initial quelconque, en choisissant un ensemble de boutons à enfoncer sur la première ligne, le reste de la procédure de récolte est déterminé. Mais cette procédure ne garantit l’extinction que des boutons des quatre premières lignes. Les ampoules de la ligne cinq peuvent rester allumées après la procédure.
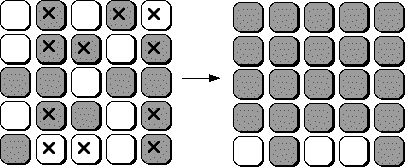
On peut alors donner la solution :
Il se pourrait toutefois qu’aucun ensemble de pressions sur la première ligne ne conduise à une solution.
La question qui reste à résoudre est : quels boutons enfoncer dans la première ligne ? Pour la résoudre, on part d’un jeu complètement éteint et on observe les résultats obtenus sur la dernière ligne pour chaque pression.
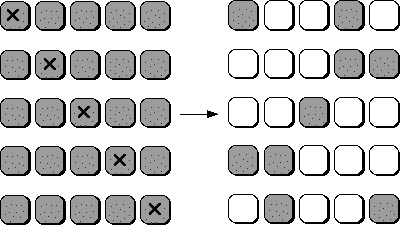
On est donc passé de la recherche parmi 25 boutons à enfoncer au cas plus simple d’une recherche parmi 5 boutons et 5 ampoules.
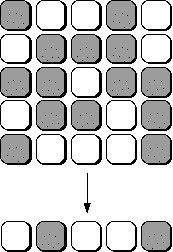
Dans un certain sens, on peut jouer maintenant avec un échiquier de dimension 1 × 5. Ce jeu hérite de certaines propriétés du jeu original : l’ordre des pressions n’est pas important et enfoncer deux fois un bouton n’a pas d’effet.
Chaque solution de ce nouveau jeu donne une solution du jeu original et réciproquement. Les états insolubles correspondent ; il en est de même pour les situations qui offrent plusieurs solutions. Les procédures pour le grand jeu sont appelées expansions de celles du petit jeu.
En observant le tableau ci-dessus, on constate que certaines configurations sont identiques :

On peut en tirer des conclusions particulièrement utiles. Ces équivalences montrent qu’il n’est jamais nécessaire d’enfoncer les deux boutons à droite : une solution faisant appel à ces deux boutons peut être remplacée par une solution équivalente ne faisant pas appel à eux. On pourrait prétendre qu’ils sont endommagés.
On constate que si deux procédures équivalentes sont exécutées à tour de rôle, une annule l’autre et le résultat final est nul. La composition des deux procédures est appelée procédure neutre.
La combinaison de n’importe quelle paire de procédures équivalentes donne deux procédures neutres. Une troisième est obtenue en combinant les deux. Il y également une quatrième procédure triviale, dans laquelle aucun bouton n’est enfoncé. Une recherche systématique montre qu’il n’y en a pas d’autres.
Une procédure quelconque suivie d’une procédure nulle est équivalente en terme de résultat obtenu. Ainsi, lorsqu’une solution est trouvée pour un état initial donné, il y a quatre autres solutions équivalentes.
On peut désormais savoir si un état est résoluble avec seulement huit essais. Mais on peut encore améliorer la solution en faisant appel à un raisonnement subtil. D’abord, le jeu a une certaine symétrie : si un bouton x permute la lumière y, alors le bouton y permute la lumière x. N’importe quelle procédure neutre fait pression sur un nombre pair de boutons dans le voisinage de n’importe quelle case en la laissant inchangée. Mais alors, par symétrie, enfoncer n’importe quel bouton permute un nombre pair de cases dans N, l’ensemble de cases enfoncées par une procédure neutre. Ainsi la parité de cases allumées dans N ne peut pas être changée par n’importe quelle pression.
De la sorte, depuis l’état complètement éteint, on ne peut obtenir des états avec un nombre pair de cases en commun avec n’importe quelle procédure neutre de N. Donc un état est résoluble seulement s’il a un nombre pair d’intersections avec n’importe quelle procédure neutre.
Pour une procédure neutre donnée, ce test diminue de moitié le nombre d’états possibles. Comme n’importe quelle procédure neutre est la composition de deux autres, il suffit de la tester pour deux d’entre elles. Ainsi, on peut diminuer de moitié le nombre d’état résolubles deux fois, et marquer trois quarts des états comme insolubles.
D’un autre côté, chaque état résoluble peut être résolu, en moyenne, par quatre différentes procédures. Ainsi un quart de états est résoluble : ceux qui passent le test précédent.
On peut choisir ces deux procédures neutres pour effectuer le test de parité :

On peut utiliser ces résultats pour montrer que l’exemple utilisé précédemment est résoluble. L’état cible avait les ampoules 1, 3 et 4 allumées ; en comparant ceci avec le premier état neutre ci-dessus, on trouve deux ampoules en commun : la troisième et la quatrième ; en comparant avec le second on obtient également un nombre pair : le premier et le troisième bouton. Ainsi l’état est résoluble :
Comment procéder alors pour résoudre un puzzle ? On sait que l’on ne s’intéresse qu’aux trois boutons à gauche de la première ligne. Leurs effets sont donnés par :
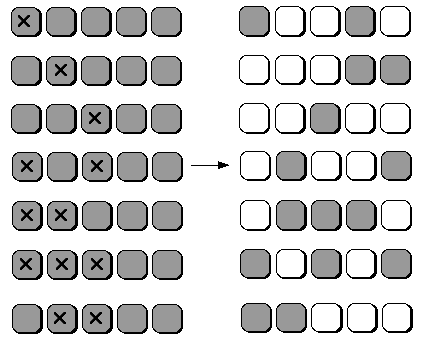
Parmi les huit possibilités de combiner les pressions sur ces trois boutons, les trois dernières combinaisons du tableau ci-dessus se distinguent. Chacune est utile puisqu’elle permute seulement une des trois lumières à gauche. Ceci procure la première façon de trouver un candidat pour une solution, sans utiliser les boutons 4 et 5. Ce candidat dépend uniquement de l’état des trois premières lumières. On l’appelle candidat plutôt que solution car on n’a aucune certitude que les derniers boutons tourneront correctement.
Une autre façon de trouver une solution consiste à observer les effets des pressions sur les trois premiers boutons.
Lights out est un problème d’algèbre matricielle. On travaille avec des vecteurs appartenant à (ℤ2)25. Soit la matrice R qui contient les règles du puzzle :
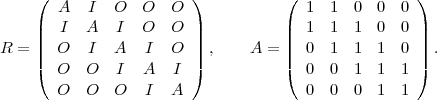
où I et O sont les matrices identité et zéro de dimension 5 × 5. Pour un
vecteur 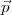 , que l’on appelle vecteur de pression, on calcule R
, que l’on appelle vecteur de pression, on calcule R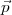 , appelé l’effet de
, appelé l’effet de 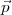 .
L’effet de
.
L’effet de 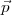 est ajouté (modulo 2) au vecteur
est ajouté (modulo 2) au vecteur 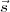 , l’état initial, pour obtenir le
nouvel état R
, l’état initial, pour obtenir le
nouvel état R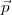 +
+ 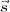 . Par exemple, avec le vecteur de pression qui dispose de uns
seulement dans le premier et le quatorzième composant, l’état nul est modifié
comme suit :
. Par exemple, avec le vecteur de pression qui dispose de uns
seulement dans le premier et le quatorzième composant, l’état nul est modifié
comme suit :
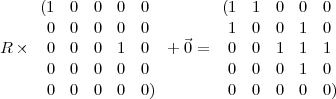
Lorsque nécessaire, les vecteurs de 25 éléments sont arrangés sous la forme
5 × 5. Le but est, étant donné un état 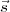 , de trouver
, de trouver 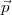 tel que R
tel que R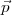 +
+ 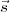 =
= 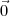 . Bien
que l’on ne parle ici que de vecteurs de 25 éléments, les méthodes peuvent être
appliquées aux vecteurs de n’importe quelle taille m × n et aux matrices
ressemblant à R.
. Bien
que l’on ne parle ici que de vecteurs de 25 éléments, les méthodes peuvent être
appliquées aux vecteurs de n’importe quelle taille m × n et aux matrices
ressemblant à R.
Une forme équivalente du problème est, étant donné 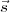 , de trouver
, de trouver 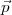 tel que
R
tel que
R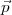 =
= 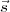 . Ceci est un problème bien connu d’algèbre. On observe que, modulo 2,
. Ceci est un problème bien connu d’algèbre. On observe que, modulo 2,
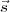 = -
= -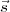 .
.
On observe qu’il est intéressant de résoudre le problème, pour un état donné
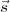 , en plusieurs étapes : en partant de l’état nul,
, en plusieurs étapes : en partant de l’état nul, 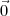 , on peut presser
, on peut presser 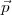 1, de sorte
que le nouvel état,
1, de sorte
que le nouvel état, 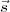 1, soit plus simple à écrire ; on presse ensuite
1, soit plus simple à écrire ; on presse ensuite 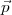 2,
etc. :
2,
etc. :
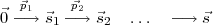
La solution serait la somme des 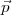 i :
i :
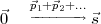
On peut utiliser les méthodes traditionnelles pour résoudre ce problème comme le calcul matriciel. Mais on essaie ici d’exploiter les particularités de R.
Le problème peut être écrit comme suit :
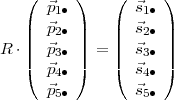
où, pour raison de clarté, 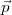 et
et 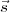 ont été divisés en sous-vecteurs
ont été divisés en sous-vecteurs 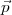 i∙ et
i∙ et 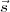 i∙,
chacun étant composé de cinq éléments.
i∙,
chacun étant composé de cinq éléments.
On manipule l’équation précédente pour la mener vers une version plus
pratique : une expression pour 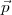 1∙ qui ne dépend que de
1∙ qui ne dépend que de 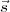 , et d’autres expressions
pour
, et d’autres expressions
pour 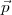 2∙…
2∙…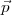 5∙ ne dépendant que de
5∙ ne dépendant que de 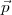 1∙ et
1∙ et 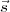 .
.
L’équation R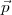 =
= 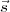 est équivalente à J
est équivalente à J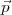 = (R + J)
= (R + J)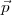 +
+ 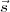 pour n’importe quelle
matrice J. Si l’on prend en particulier :
pour n’importe quelle
matrice J. Si l’on prend en particulier :
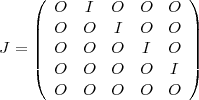
on trouve :
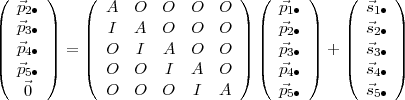
Ici, chaque 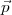 i∙ dépend seulement des sous-vecteurs de
i∙ dépend seulement des sous-vecteurs de 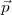 et
et 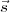 avec des indices
plus petits que le sien. Ainsi, on peut utiliser l’équation de la première ligne pour
ôter
avec des indices
plus petits que le sien. Ainsi, on peut utiliser l’équation de la première ligne pour
ôter 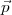 2∙ de la deuxième ensuite, on utilise la deuxième ligne pour éliminer
2∙ de la deuxième ensuite, on utilise la deuxième ligne pour éliminer 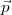 3∙ de
la troisième, etc.
3∙ de
la troisième, etc.
Ainsi, 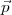 2∙…
2∙…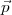 5∙ sont définis uniquement par
5∙ sont définis uniquement par 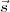 et
et 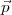 1∙ :
1∙ :
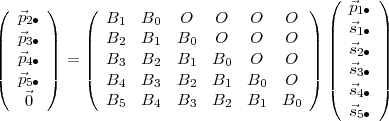
où B0 = I, B1 = A et Bn+2 = A × Bn+1 + Bn. Maintenant l’équation
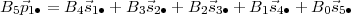
prise de la dernière ligne de la matrice précédente, ne tient compte que de 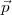 i∙,
partie de
i∙,
partie de 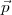 .
.
On peut donc travailler avec cette équation en trois étapes :
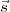 ; on appelera ce vecteur, récolte(
; on appelera ce vecteur, récolte(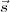 ) ;
) ;
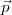 1∙ tel que B5
1∙ tel que B5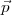 1∙ est égal à récolte(
1∙ est égal à récolte(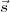 ) qui
est connu ;
) qui
est connu ;
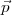 2∙…
2∙…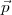 5∙ directement depuis
5∙ directement depuis 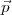 1∙ et
1∙ et 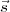 , en utilisant
les équations des quatre lignes du haut de la matrice précédente.
, en utilisant
les équations des quatre lignes du haut de la matrice précédente. Il existe des 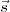 pour lesquels aucun
pour lesquels aucun 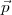 1∙ ne satisfait l’équation ci-dessus. Dans
ces cas, le problème n’a pas de solution.
1∙ ne satisfait l’équation ci-dessus. Dans
ces cas, le problème n’a pas de solution.
La question qui reste est de savoir comment obtenir 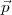 1∙ qui satisfasse
l’équation
1∙ qui satisfasse
l’équation
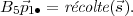
La matrice B5 est la suivante :
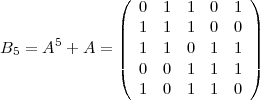
Les dépendances linéaires trouvées nous permettent de voir le problème en dimension 25 comme un problème de dimension 5. Comme exemple, l’état suivant est réduit afin de passer à un problème plus simple :

après récolte :
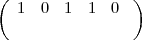
Chaque solution à ce problème donne une et une seule solution au problème original et vice versa. On appelle les vecteurs de 25 éléments des extensions des vecteurs de 5 éléments :
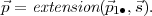
On peut exécuter une réduction de Gauss-Jordan sur B5 pour obtenir XB5 = E et on obtient :


On note que null(E) égale null(B5) et sa dimension est 2, donc c’est le cas pour null(R). Les vecteurs suivant produisent une base de null(E) :
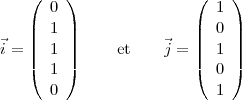
Ceci nous permet de générer d’autres solutions : si 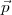 est une solution pour
est une solution pour 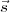 ,
alors les trois autres solutions sont :
,
alors les trois autres solutions sont :
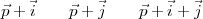
En observant les vecteurs 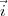 et
et 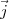 , on remarque qu’une de ces solutions aura des
zéros dans les quatrième et cinquième éléments.
, on remarque qu’une de ces solutions aura des
zéros dans les quatrième et cinquième éléments.
On peut réduire la recherche des solution aux vecteurs de dimension trois. Ainsi, seulement 23 états peuvent être recherchés parmi le total possible de 25. En d’autres mots, l’image de notre matrice a une dimension trois ; on le sait car l’ordre de la matrice carrée (de dimension 5 dans l’exemple) égale la dimension de son espace nul (2) plus la dimension de son image. Chaque état n’est pas résoluble ; il est donc intéressant d’identifier des critères pour trouver les états résolubles.
L’algèbre nous dit que, étant donné une matrice symétrique (comme B5), son
image est orthogonale à son espace nul. Ainsi, pour un état donné 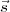 , il
existe une solution
, il
existe une solution 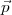 pour l’équation B5
pour l’équation B5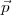 =
= 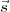 si et seulement si
si et seulement si 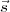 est
orthogonal à l’espace nul de la matrice. Le produit scalaire
est
orthogonal à l’espace nul de la matrice. Le produit scalaire 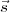 ×
×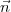 doit
être égal à zéro pour chaque
doit
être égal à zéro pour chaque 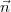
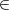 null(B5). Ceci concerne les équations
suivantes :
null(B5). Ceci concerne les équations
suivantes :
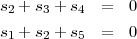
Considérons cette explication pour montrer que l’exemple montré plus haut est résoluble. On calcule le produit scalaire de l’état considéré avec les deux procédures neutres. On trouve pour chacun un résultat nul, ce qui signifie que les deux équations ci-dessus sont satisfaites. Donc l’état est résoluble.
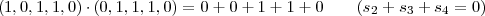
et
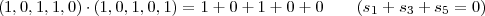
En utilisant la réduction de Gauss-Jordan pour B5, on a obtenu :
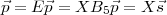
Ceci permet de calculer une solution aisément ; les trois autres sont obtenues
en additionnant les vecteurs de l’espace nul de la matrice 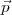 .
.
En reprenant la matrice
On peut exprimer les solutions comme suit :
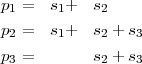
En résumé, pour calculer la solution d’un état 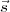 de 25 éléments du problème
non réduit, on calcule les trois premiers éléments de récolte(
de 25 éléments du problème
non réduit, on calcule les trois premiers éléments de récolte(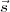 ) ; ensuite on
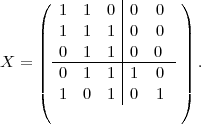
recherche p1, p2 et p3 ; ensuite, finalement la solution expansion(
) ; ensuite on
recherche p1, p2 et p3 ; ensuite, finalement la solution expansion(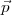 1∙,
1∙,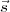 ).
).
La solution actuellement proposée est donnée par les fichiers MatLab : ligthsOut.m et c_ligthsout.m.