Résumé : Comment placer plusieurs sphères dans un cylindre comme des boules de glaces dans un cornet ? Germinal Pierre Dandelin s’est posé cette question en 1822. Il a même formulé un théorème qui porte son nom.
Mots-clés : sphère, cône, ellipse, tangente, foyer.
L’exercice s’inspire du livre Mathematic in Action de Stan Wagon, Springer, New York, 1999 et de divers sites Internet.
La construction connue sous le nom de sphères de Dandelin peut être décrite comme suit. On laisse tomber deux sphères inégales dans un cône, la plus petite en premier et la plus grande ensuite —suffisamment grande pour être arrêtée par le cône avant de toucher la plus petite. On considère le plan qui coupe le cône de sorte qu’il soit également tangent aux deux sphères. L’intersection est une ellipse. La surprise réside dans le fait que les points de tangence aux sphères sont les foyers de l’ellipse !
Le but du problème est de représenter un cône et deux sphères dont les dimensions peuvent être changées. Le plan d’intersection et l’intersection avec le cône peuvent également être représentés.
Dans l’exemple ci-dessous, un des foyers de l’ellipse est également ajouté à la représentation graphique.

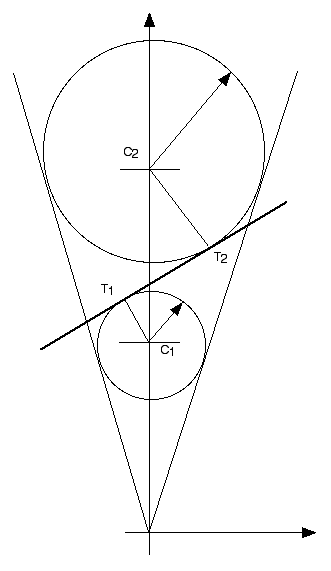
Pour résoudre ce problème, il peut être utile de passer par une projection sur un plan vertical. Les variables sont les rayons des sphères r1 et r2 et la pente m du côté du cône.
A partir de ces données, on peut déduire les hauteurs des centres des sphères h1 et h2, les coordonnées des centres C1 et C2, le point d’intersection M du plan tangent avec l’axe de symétrie du cône, les distances du point M aux centres MC1 et MC2 et les points tangents aux sphères T1 et T2.
Les équations sont données ci-dessous :
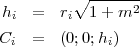
Pour calculer MC1, on résout les équations suivantes :
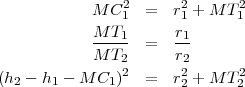
On obtient alors :
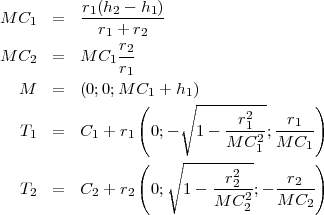
Pour dessiner le cône, on considère :
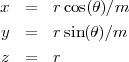
Pour la sphère, on prend :
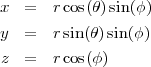
Pour construire le plan et l’ellipse, il faut calculer l’équation du plan (z en fonction de y). On la déduit de l’équation de la droite qui passe par M, T1 et T2 :
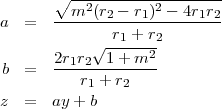
Puis on calcule l’intersection entre le plan et le cône :
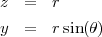
On en déduit l’équation de l’ellipse :
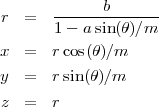
Les foyers sont données par les expressions ci-dessus.
Pour démontrer le théorème de Dandelin, il suffit de choisir un point M de l’ellipse. On trace la génératrice du cône passant par le sommet du cône et par M. Cette génératrice est tangente aux deux sphères en P et Q. Les segments MA et MP sont égaux puisqu’ils sont tous les deux tangents à la même sphère et issus du même point M. Les segments MB et MQ sont égaux pour la même raison. On en déduit :
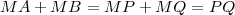
Comme la longueur du segment PQ est constante quelque soit le point M (puisque P et Q sont définis par les deux cercles parallèles de contact des sphères dans le cône), on vient de montrer que les points A et B sont tels que pout tout point M de l’ellipse :
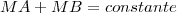
Donc les points A et B sont bien les foyers de l’ellipse.
Pour ceux qui désirent connaître mieux Dandelin, Germinal Pierre Dandelin est né au Bourget le 12 avril 1794 ; il est décédé à Bruxelles le 15 février 1847.
Le père de Dandelin était administrateur français, mais sa mère était originaire du Hainaut. Dandelin étudia à Gand et, en 1813, il entra à l’Ecole Polytechnique de Paris. Toutefois sa carrière allait être influencée par les événements politiques de cette période troublée. En 1813 Dandelin se porta volontaire pour combattre les Anglais. En mars 1814, le Traité de Chaumont réunit l’Autriche, la Russie, la Prusse et la Grande Bretagne dans le but de battre Napoléon. Quand les forces alliées arrivèrent à proximité de Paris le 30 mars 1814, Dandelin, qui combattait dans l’armée française, fut blessé. Napoléon abdiqua le 6 avril, mais revint l’année suivante pendant la campagne des 100 jours. Pendant le retour de Napoléon en France, Dandelin travailla au ministère de l’Intérieur sous les ordres de Carnot. Après la défaite de Napoléon à Waterloo, Dandelin retourna en Belgique.
Il devint citoyen néerlandais en 1817. De retour en Belgique, Dandelin continua sa carrière militaire comme ingénieur. A partir de 1825 il passa cinq ans comme professeur d’exploitation des mines à Liège. Ensuite, en 1830, il fut en plein cœur de la révolution. A partir de 1835, il fut en charge dans l’armée belge des fortifications à Namur, à Liège et plus tard à Bruxelles. Dans le domaine mathématique, Dandelin fut influencé par Quételet, son cadet de deux ans, et ses premiers intérêts allèrent à la géométrie. Dandelin découvrit en 1822 un théorème important relatif aux sections d’un cône par un plan et aux sphères inscrites. Ce théorème montre qu’une section plane est une conique dont les foyers sont les points de contact des sphères inscrites. En 1826 il généralisa son théorème à un hyperboloïde de révolution, en montrant les relations entre les théorèmes de Pascal, Brianchon et l’hexagone formé par les génératrices de l’hyperboloïde. Dandelin travailla également à la projection stéréographique d’une sphère sur un plan (1827), à la statique, à l’algèbre et aux probabilités. Il donna une méthode de calcul approché des racines d’une équation algébrique, nommée actuellement méthode de Dandelin-Gräffe.
Parmi les distinctions qui l’honorèrent, Dandelin fut élu à l’Académie Royale des Sciences de Bruxelles en 1825.
La solution actuellement proposée est donnée par les fichiers MatLab : dandelin.m.