Résumé : parfois, les hommes ont tenté de construire des puzzles tridimensionnels. Il n’y en ait aucun qui a eu autant de succès que le cube SOMA inventé par l’auteur danois Piet Hein. Parmi les quelques millions de possibilités, il n’y en a que 240 correctes qu’un logiciel, muni d’un bon algorithme, peut trouver.
Mots-clés : cube, combinatoire, symétrie.
L’exercice s’inspire du site internet de Thorleif Bundgård :
http://www.fam-bundgaard.dk/SOMA/SOMA.HTM
Parfois, les hommes ont tenté de construire des puzzles tridimensionnels. Il n’y en a aucun qui a eu autant de succès que le cube SOMA inventé par l’auteur danois Piet Hein, en 1936, pendant un cours de physique quantique donnée par Werner Heisenberg. Lorsque le sujet suivant fut traité : « une salle divisée en cubes », Piet Hein laissa courir son imagination et proposa cette nouvelle théorie géométrique.
Si vous prenez toutes les formes irrégulières possibles qui peuvent être combinées avec moins de quatre cubes, de même taille et réunis par leurs faces, alors ces formes peuvent, en s’assemblant, former un cube plus grand. Il y a douze possibilités de combiner moins de quatre cubes. Le terme « irrégulier » signifie dans de telles formes que l’on peut joindre deux points par un trait qui se trouve à l’extérieur (sauf pour les extrémités). Ainsi, une forme formée de trois cubes alignés n’est pas irrégulière.
Piet Hein se convint rapidement qu’il n’y avait que sept formes, pour un total de vingt-sept cubes, qui pourraient former en se combinant un cube plus grand de dimension 3 × 3 × 3. Piet Hein nomma son ensemble de formes, SOMA. Le mot soma vient du sanskrit ; il s’agit de l’extraction d’une plante euphorisante utilisée dans l’Inde ancienne.
Il est intéressant de noter que Piet Hein n’a pas commencé en découpant un cube pour former un puzzle mais, en visualisant les formes avant de les assembler. Piet Hein et ses successeurs ont remarqué que le placement des formes était très intéressant mais également très prenant. Des psychologues ont tenté une comparaison entre la facilité à résoudre le cube SOMA et l’intelligence : généralement les courbes se recoupent mais, certains génies obtiennent des résultats pathétiques alors que certains attardés mentaux disposent de dons spéciaux pour le faire.
Il y a 240 façons de résoudre le cube SOMA. Mais il y a également toute une panoplie de formes nouvelles : pyramide, baignoire, chien, etc.
Une activité évidente consiste à trouver toutes les solutions possibles. Le but du problème consiste à écrire un programme permettant de les trouver et de les représenter.

Piet Hein (1905-1996) était un poète et scientifique danois avec de nombreux intérêts. Ses poèmes, connus sous le nom de « Grooks », furent écrits en 1940 lorsque les nazis envahirent le Danemark. A cette époque, il était président de l’union anti-nazie, dut se cacher, et en profita pour écrire sa poésie. Piet Hein était un génie avec plusieurs facettes. En plus du cube soma, il créa une nouvelle forme géométrique, la super-ellipse, un objet entre le rectangle et l’ellipse. Dans les années 50 et 60, il trouva de magnifiques formes aux meubles et contribua ainsi à l’essor du design scandinave.
Le nom, Soma, est tiré de la nouvelle d’Aldous Huxley, Brave New World. Cette nouvelle décrit une société du futur dans laquelle, le Soma est une drogue addictive apparemment destinée aux personnes de l’establishment lorsqu’elles s’ennuyaient.
Le jeu Soma est distribué depuis 1970 par Parker Bros Co.
Pour trouver les sept pièces du puzzle, on peut considérer les critères suivants :
La première règle nous indique qu’il y a une figure formée d’un cube unique (un demi-sucre), une figure formée de deux cubes (domino), deux figures formées de trois cubes (l’hexaèdre peut être éliminé) et huit figures formées de quatre cubes : quatre cubes formant un carré, quatre cubes alignés (un bâton) et six autres combinaisons. Les deux premières combinaisons sont régulières alors que les six dernières sont irrégulières. Il reste donc sept pièces. Elles peuvent être assemblées pour former un cube de dimension 3 × 3 × 3.
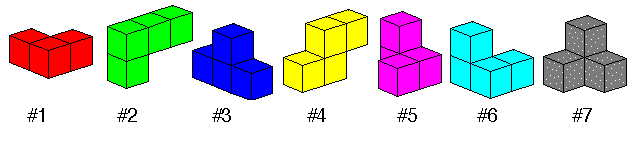
Il n’y a que 240 solutions standards pour résoudre ce problème si l’on élimine les rotations et les effets de miroir. Il y a 24 façons de tourner le cube assemblé et chaque rotation permet un effet de miroir. Ceci nous amène à 240 × 24 × 2 = 11′520. De plus cinq pièces (#1,#3,#4,#5 et #6) peuvent être ôtées du cube, tournées pour ressembler à elles-mêmes et replacées exactement. La pièce #7 peut être tournée de trois façons différentes, ce qui multiplie le nombre de solutions d’un facteur 25 × 3 = 96. On a donc, au total, 1′105′920 solutions.
Thorleif Bundgård et Courtney McFarren ont mis à disposition des internautes un logiciel écrit en QBasic, (solve121.exe), ainsi que les sources, (solve121.bas), et une description des algorithmes utilisés.
Une structure Soma est toujours formée de vingt-sept cubes unitaires. On affecte au départ un nombre de 1 à 27 à chaque cube. Ainsi, pour le grand cube 3 × 3 × 3, on numérote ainsi :
| (1,1)1 | (1,2)2 | (1,3)3 |
| (2,1)4 | (2,2)5 | (2,3)6 |
| (3,1)7 | (3,2)8 | (3,3)9 |
| (4,1) |
la couche de base,
| (1,1)10 | (1,2)11 | (1,3)12 |
| (2,1)13 | (2,2)14 | (2,3)15 |
| (3,1)16 | (3,2)17 | (3,3)18 |
| (4,1) |
la couche centrale, et
| (1,1)19 | (1,2)20 | (1,3)21 |
| (2,1)22 | (2,2)23 | (2,3)24 |
| (3,1)25 | (3,2)26 | (3,3)27 |
| (4,1) |
la couche du haut.
Ensuite, on prend la pièce #1, on la déplace et on la tourne à l’intérieur de la structure et de toutes les façons possibles. On obtient alors une liste de toutes les positions possibles :
| (1,1)1 | (1,2)4 | (1,3)5 |
| (2,1)1 | (2,2)4 | (2,3)2 |
| (3,1)4 | (3,2)2 | (3,3)5 |
| (4,1)1 | (4,2)2 | (4,3)5 |
| (5,1)2 | (5,2)5 | (5,3)6 |
| (6,1)2 | (6,2)5 | (6,3)3 |
| (7,1)5 | (7,2)3 | (7,3)6 |
| (8,1)2 | (8,2)3 | (8,3)6 |
| (9,1)4 | (9,2)7 | (9,3)8 |
| (10,1)4 | (10,2)7 | (10,3)5 |
| (11,1).... |
Pour la deuxième, on a le début de liste suivant :
| (1,1)1 | (1,2)2 | (1,3)5 | (1,4)8 |
| (2,1)1 | (2,2)4 | (2,3)7 | (2,4)2 |
| (3,1)7 | (3,2)2 | (3,3)5 | (3,4)8 |
| (4,1)1 | (4,2)4 | (4,3)7 | (4,4)8 |
| (5,1)2 | (5,2)3 | (5,3)6 | (5,4)9 |
| (6,1)2 | (6,2)5 | (6,3)8 | (6,4)3 |
| (7,1)8 | (7,2)3 | (7,3)6 | (7,4)9 |
| (8,1)2 | (8,2)5 | (8,3)8 | (8,4)9 |
| (9,1)10 | (9,2)11 | (9,3)14 | (9,4)17 |
| (10,1)10 | (10,2)13 | (10,3)16 | (10,4)11 |
| (11,1).... |
On fait de même pour les pièces de 3 à 7. Comme il y a environ une centaine de possibilités par pièce, il y a de l’ordre de 1007 combinaisons possibles. Il faut donc trouver des algorithmes permettant de raccourcir la recherche.
Le premier test qui peut être appliqué concerne les intersections : on considère la première entrée dans la liste de la pièce #1 (1-4-5), on prend alors une pièce dans la liste #2. Il est inutile de prendre des positions qui ont des intersections avec la première pièce. On peut prendre, par exemple, (2-3-6-9). On poursuit ce raisonnement avec les pièces #3 à #7. Si toutes les positions ont été testées sans succès on remonte à la pièce #1 et on recommence avec la position suivante : (1-4-2).
Un autre test permet de raccourcir le temps de la recherche : le test des îlots. Si l’on considère une structure originale, par exemple, un banc. La figure est formée de deux lignes de 9 cubes pour la couche du bas et une ligne de 9 cube pour la couche du haut. Si l’on place la pièce #1 au milieu de la structure, on constate la formation de deux îlots, l’un avec neuf cubes et l’autre avec quinze cubes. Comme les pièces restantes sont formées de quatre cubes chacune, il est impossible de remplir les îlots restants. Il faut donc un multiple de quatre pour terminer le problème. Ceci permet évidemment de diminuer le nombre de configurations à tester.
Les auteurs mentionnés plus haut proposent également d’ajouter un test de parité : si l’on colore chaque cube en noir et en blanc comme suit :
| (1,1)B | (1,2)W | (1,3)B |
| (2,1)W | (2,2)B | (2,3)W |
| (3,1)B | (3,2)W | (3,3)9 |
| (4,1) |
la couche de base,
| (1,1)W | (1,2)B | (1,3)W |
| (2,1)B | (2,2)W | (2,3)B |
| (3,1)W | (3,2)B | (3,3)W |
| (4,1) |
la couche centrale, et
| (1,1)B | (1,2)W | (1,3)B |
| (2,1)W | (2,2)B | (2,3)W |
| (3,1)B | (3,2)W | (3,3)B |
| (4,1) |
la couche du haut.
Alors la parité est définie comme le nombre de noirs moins le nombre de blancs. Ici on a 14 - 13 = +1. Pour chaque pièce, on a les possibilités suivantes :
Pour la pièce #1 :
| (1,1)B | (1,2) |
| (2,1)W | (2,2)B |
| (3,1) |
avec comme parité 2 - 1 = +1 et
| (1,1)W | (1,2) |
| (2,1)B | (2,2)W |
| (3,1) |
avec parité : 1 - 2 = -1.
La pièce #2 a toujours la parité 0 :
| (1,1)B | (1,2)W | (1,3)B |
| (2,1)W | ||
| (3,1) |
et
| (1,1)W | (1,2)B | (1,3)W |
| (2,1)B | ||
| (3,1) |
La pièce #3 peut avoir la parité 2 ou -2. Les pièces #4, #5 et #6 ont toujours la parité 0 et enfin, la pièce #7 peut avoir la parité 2 ou -2. En résumé, seules les pièces #1, #3 et #7 ont une parité non nulle. Si l’on fait un tableau de toutes les possibilités, on remarque :
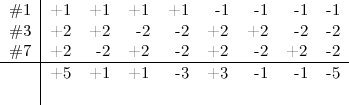
Donc, si une structure a une parité de 1, -3 ou +5, alors la pièce #1 doit être de parité 1, sinon, elle est de parité -1. Ainsi, parmi les 144 possibilités de placer la première pièce, il n’en reste plus que 72.
Le nombre de possibilités de placer chaque pièce est le suivant :
| (1,1)#1 | (1,2)144 | (1,3) | (1,4)#2 | (1,5)144 |
| (2,1)#3 | (2,2) 72 | (2,3) | (2,4)#4 | (2,5) 72 |
| (3,1)#5 | (3,2) 96 | (3,3) | (3,4)#6 | (3,5) 96 |
| (4,1)#7 | (4,2) 64 | (4,3) | (4,4) | (4,5) |
| (5,1) |
En permutant l’ordre des pièces, on peut encore gagner du temps. Il est conseillé de prendre l’ordre suivant : 1-7-3-4-5-6-2.
La solution actuellement proposée est donnée par les fichiers MatLab : somaConstr.m, dessineSoma.m et demoSoma.m.