Résumé : La conceptualisation de l’infini pose des problèmes depuis longtemps. Une représentation graphique originale permet d’illustrer ce concept à partir de recherches publiées en 1938 par L. R. Ford : un ensemble de sphères construites à partir des cercles de Ford. Chaque sphère est entourée d’une chaîne infinie de sphères qui l’embrassent.

Mots-clés : Farey, Ford, sphère, infini, fractal, nombre complexe, fraction complexe.

Solutions :

La solution actuellement proposée est donnée en P5JS.

thèmes

de plus

Le baiser infini

L’exercice s’inspire du livre Wonders of Numbers, Adventures in Mathematics, Mind, and Meaning de Clifford A. Pickover, Oxford University Press, 2001 et du site Internet www.cut-the-knot.com.

John Farey (1766-1826) est un biologiste britannique. Il s’est intéressé à une propriété curieuse des fractions « vulgaires » : « Si toutes les fractions possibles, dont le plus grand dénominateur ne dépasse pas un nombre donné, sont arrangées dans l’ordre croissant, alors si le numérateur et le dénominateur sont ajoutés au numérateur et au dénominateur respectivement de l’antépénultième fraction, les sommes obtenues sont celles de la pénultième fraction (ce raisonnement peut être appliqué des deux côtés).

Par exemple, si 5 est le plus grand dénominateur, toutes les fractions possibles triées dans l’ordre croissant sont : 1∕5, 1∕4, 1∕3, 2∕5, 1∕2, 3∕5, 2∕3, 3∕4 et 4∕5. Si l’on considère la fraction 1∕3, alors en ajoutant l’antépénultième fraction 1∕5, on obtient (1 + 1)∕(3 + 5) = 2∕8 = 1∕4 qui se trouve entre le deux. En prenant la fraction à droite 1∕2, la somme obtenue est alors (1 + 1)∕(3 + 2) = 2∕5 qui se trouve comprise entre les deux dans la liste. L’ensemble de toutes les fractions réduites dans l’intervalle fermé [0;1] avec dénominateurs ne dépassant pas n, trié dans l’ordre croissant, est connu sous le nom de suite de Farey d’ordre n et est noté F_n.

Par exemple,

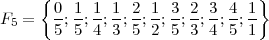
Soient trois fractions consécutives de la suite de Farey d’ordre n, a∕b, a′∕b′ et a′′∕b′′, alors a′∕b′ = (a + a′′)∕(b + b′′).

Une interprétation géométrique permet de visualiser ce concept. Elle est l’œuvre de L. R. Ford qui, en 1938, proposa d’utiliser des cercles : pour un point P (dont la valeur est p∕q) sur l’axe des x, on prend 1∕q² comme diamètre et (p∕q;1∕(2y²) comme coordonnées du centre ; on construit un cercle tangent à l’axe des x au point donné. Le cercle construit est appelé cercle de Ford.

Pour une suite de Farey donnée d’ordre n, si l’on représente toutes les fractions sur l’axe des x par le cercle de Ford correspondant, on obtient un ensemble de cercles qui se touchent.

Il est particulièrement étonnant d’observer que les cercles de Ford sont soit séparés soit tangents. Ils ne se coupent jamais.

Il est particulièrement étonnant d’observer que les cercles de Ford sont soit séparés soit tangents. Ils ne se coupent jamais.

Clifford A. Pickover a eu l’idée de remplacer les cercles de Ford par des sphères. En partant de la fraction p∕q, on représente une sphère dont les coordonnées du centre sont (p∕q;1∕(2q2);0) et le rayon est 1∕(2q2). Pour des raisons esthétiques, on représente également la sphère obtenue par effet d’un miroir vertical. On observe que les sphères ne se coupent jamais et que chaque sphère est entourée par une infinité de sphères.

On peut imaginer un archer qui lance une flèche en direction des sphères de Ford. Suivant sa trajectoire, la flèche pourra se comporter différemment : si l’archer envoie une flèche perpendiculairement à une sphère qui touche l’axe des x à une fraction, alors la flèche traverse la sphère et ressort au point exact de tangence ; si la flèche est envoyée vers un point irrationnel de l’axe des x, alors elle devra entrer dans une sphère, en ressortir, entrer dans une autre sphère, en ressortir, indéfiniment.

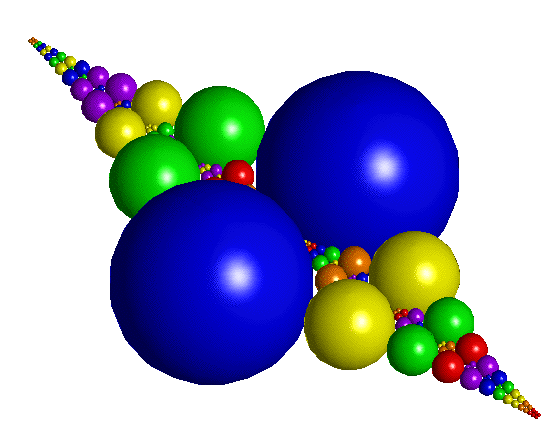
Clifford A. Pickover a repris cette idée et l’a adaptée aux fractions complexes. Les fractions complexes sont de la forme p∕q où p et q sont des nombres complexes de la forme a + ib, où i = 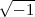et a et b des entiers.

Ainsi, si p = p′ + ip′′ et q = q′ + iq′′, alors

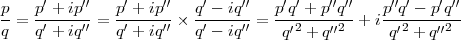
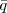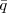Les fractions complexes sont donc également des nombres complexes de la forme x + iy avec x et y des fractions réelles. En poursuivant l’idée de Ford, on peut construire une sphère qui représente la fraction p∕q : elle touche le plan complexe à la position p∕q et a un rayon 1∕(2q ) où est le complexe conjugué de q (soit un nombre complexe a + ib, alors le complexe conjugué est a - ib).

Une question se pose : combien de sphères touchent une sphère individuelle ? Deux fractions sont adjacentes si leurs sphères sont adjacentes. Chaque fraction dispose d’une infinité de voisines donc, chaque sphère dispose d’une infinité de sphères adjacentes. On peut montrer que, si deux sphères sont placées aux fractions complexes P∕Q et p∕q, alors elles sont tangentes si |Pq - pQ| = 1.

L’ordinateur est capable de représenter de manière magnifique les fractions complexes. Avec les outils actuels, on peut éclairer les sphères, les rendre transparentes, simuler un matériau réfléchissant. Le but de ce problème est donc de représenter quelques sphères de cette suite infinie.

En modifiant les paramètres, on peut obtenir d’autres représentations originales des fractions complexes.

Indications

Pour fabriquer une suite de Farey, il suffit de considérer toutes les fractions possibles entre 0∕n et n∕n = 1∕1. On vérifie que le dénominateur est plus petit que le numérateur et que leur plus grand commun diviseur est un. De la sorte, on s’assure que les fractions soient irréductibles. Ensuite, il suffit de trier la suite des fractions.

La preuve de la propriété des suites de Farey peut s’énoncer comme suit : soit m₁∕n₁ et m₂∕n₂ deux termes successifs de la série, alors m₂n₁ = m₁n₂. Ce résultat découle de l’algorithme d’Euclide permettant de calculer le plus grand commun diviseur de deux nombres non premiers entre eux : si b divise a, alors le plus grand commun diviseur de a et b est b ; si a = bt + r, avec t et r entiers, alors le plus grand commun diviseur de a et b est égal au plus grand commun diviseur de b et r (le PGCD de 96 et 81 se calcule comme suit : 96 = 1 ⋅ 81 + 15, 81 = 5 ⋅ 15 + 6, 15 = 2 ⋅ 6 + 3. 6 = 2 ⋅ 3 + 0, donc le PGCD vaut 3). Un corollaire de cet algorithme est : pour chaque paire de nombre entiers a et b, il existe deux entiers s et t tels que as + bt = PGCD(a,b).

Dans la suite de Farey, en prenant trois fractions consécutives, le terme médian est donné par :

Pour le démontrer, on part des deux égalités :

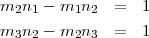
En soustrayant les deux lignes :

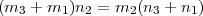
ce qui prouve la définition du terme médian.

Pour les cercles de Ford, on considère deux fractions a∕b et c∕d qui définissent deux cercles qui se touchent. Alors, le cercle correspondant à la fraction médiane (a + c)∕(b + d) est tangent aux deux. La preuve est basée sur le fait que les deux cercles correspondants à a∕b et c∕d se touchent si et seulement si ac et bd sont des entiers consécutifs.

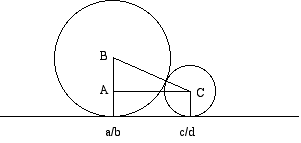
Dans le graphique, on considère que b < d et que a∕b < c∕d. Du triangle ABC, on déduit : 2 ⋅ AB = 1∕b² - 1∕d² et 2 ⋅ BC = 1∕b² + 1∕d² et AC = c∕d - a∕b. Par le thérème de Pythagore, bc - ad = 1. Ceci implique à la fois (b + d)c - (a + c)d = 1 et (a + c)b - (b + d)a = 1. Donc, le cercle médian touche les deux autres si et seulement s’ils sont tangents l’un l’autre.

On peut tenir exactement le même raisonnement pour les sphères. La distance AC est fonction de CB. Donc,

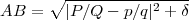
où

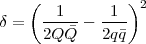
Donc,

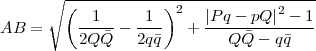
Si > 1, alors les sphères ne se touchent pas. Si = 1, alors les sphères P∕Q et p∕q se touchent.

Version P5JS. Instructions: '+' augmente le niveau, '-'' diminue le niveau, 'a', affiche des couleurs aléatoires et 'c', affiche avec relief.