résumé
thèmes
Être de Mesh le maillage se dit Mesh en anglais. Il consiste à décomposer l’enveloppe d’un volume en polygones. De belles surfaces peuvent ainsi être représentées.
Jouer à la bataille navale tout seul: retrouver des navires cachés dans un océan représenté par une grille en se basant sur quelques indices, c'est le but du jeu de la navale en solitaire ou bimaru.
Le jeu de quinze: le jeu du quinze est très simple: il faut sélectionner trois chiffres (parmi les chiffres entre 1 et 9) dont le total donne quinze. Votre adversaire en fait de même. Un ordinateur peut jouer ce rôle et vous rendre la tâche plus difficile ou plus facile.
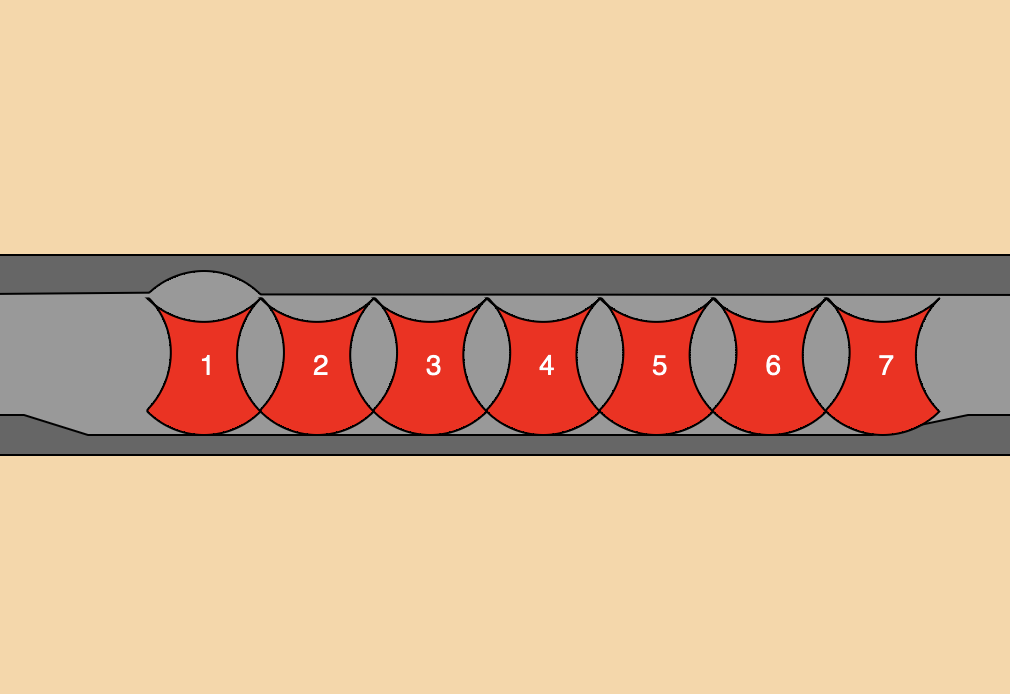
Programmer des pâtes: cuisiner des pâtes à l’italienne et s’apercevoir que derrière chacune d’elles se cache une équation mathématique est une belle découverte. Avec un ordinateur, il est possible alors de reproduire près d’une centaine de pâtes différentes et de les visualiser grâce aux représentations 3D
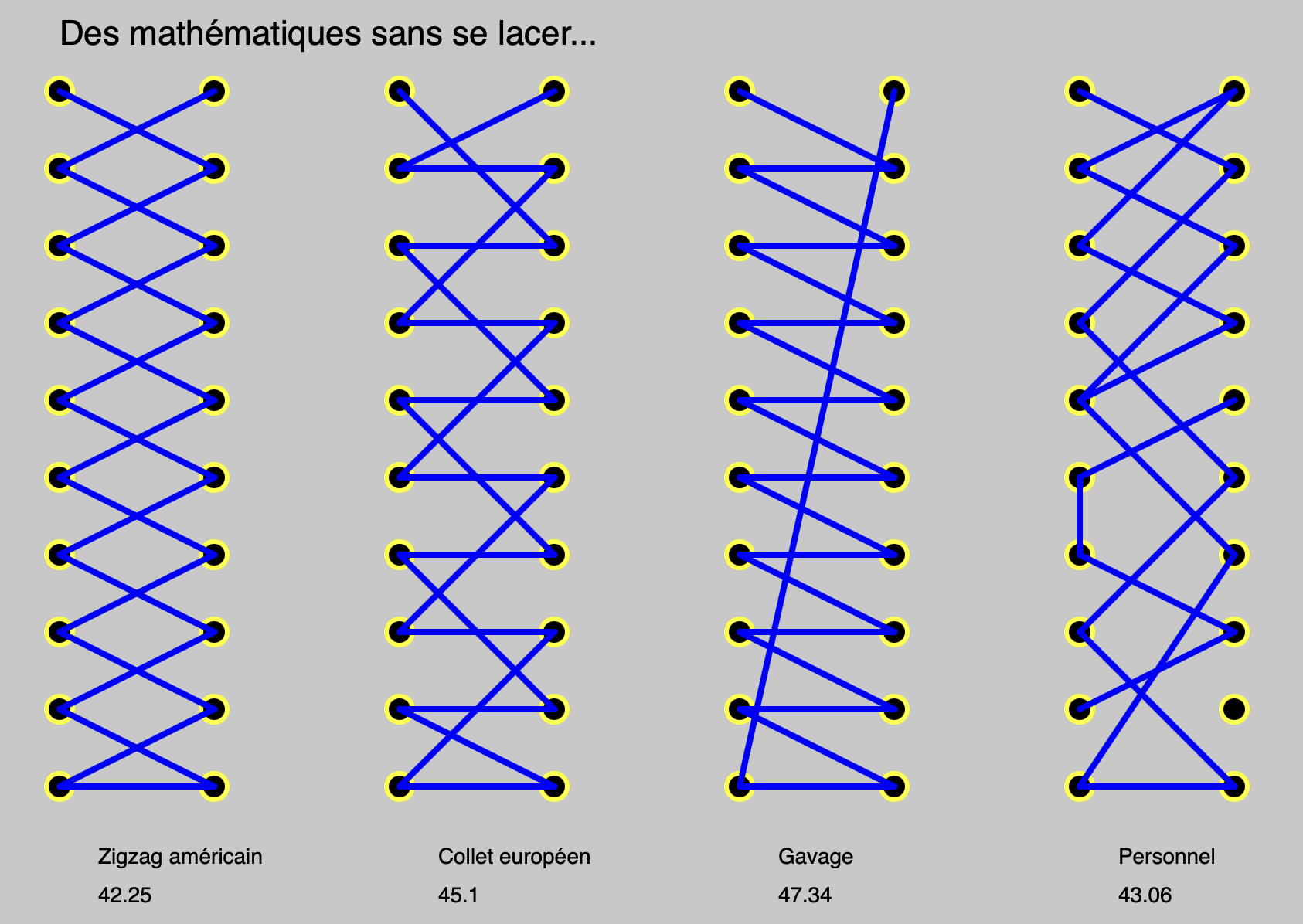
Mathématiques sans se lacer: Quelle est la façon de lacer la plus économique? A l’époque de la globalisation, la question peut préoccuper les gestionnaires mais, les mathématiques peuvent les aider.
Vigne noble: observer une vigne depuis un véhicule en mouvement est une expérience intéressante. Une forme d’illusion apparaît: certains ceps et piquets semblent apparaître et disparaître suivant le mouvement du véhicule.
De l’utilité d’une calculette endommagée: peut-on ou doit-on utiliser une calculette en classe? Pour alimenter ce débat, Alex Bogolmony suggère de donner aux élèves une calculette endommagée et d’observer leur comportement: font-ils alors appel à leurs connaissances pour se débrouiller?
Des spirales et des fleurs: un capitule de tournesol, comme celui d’une pâquerette, ou bien les dispositions des écorces des pommes de pin présentent des familles de spirales qui s’interpénètrent. Le sens d’enroulement étant opposé. Des modélisations permettent de reproduire ce phénomène particulièrement fascinant.
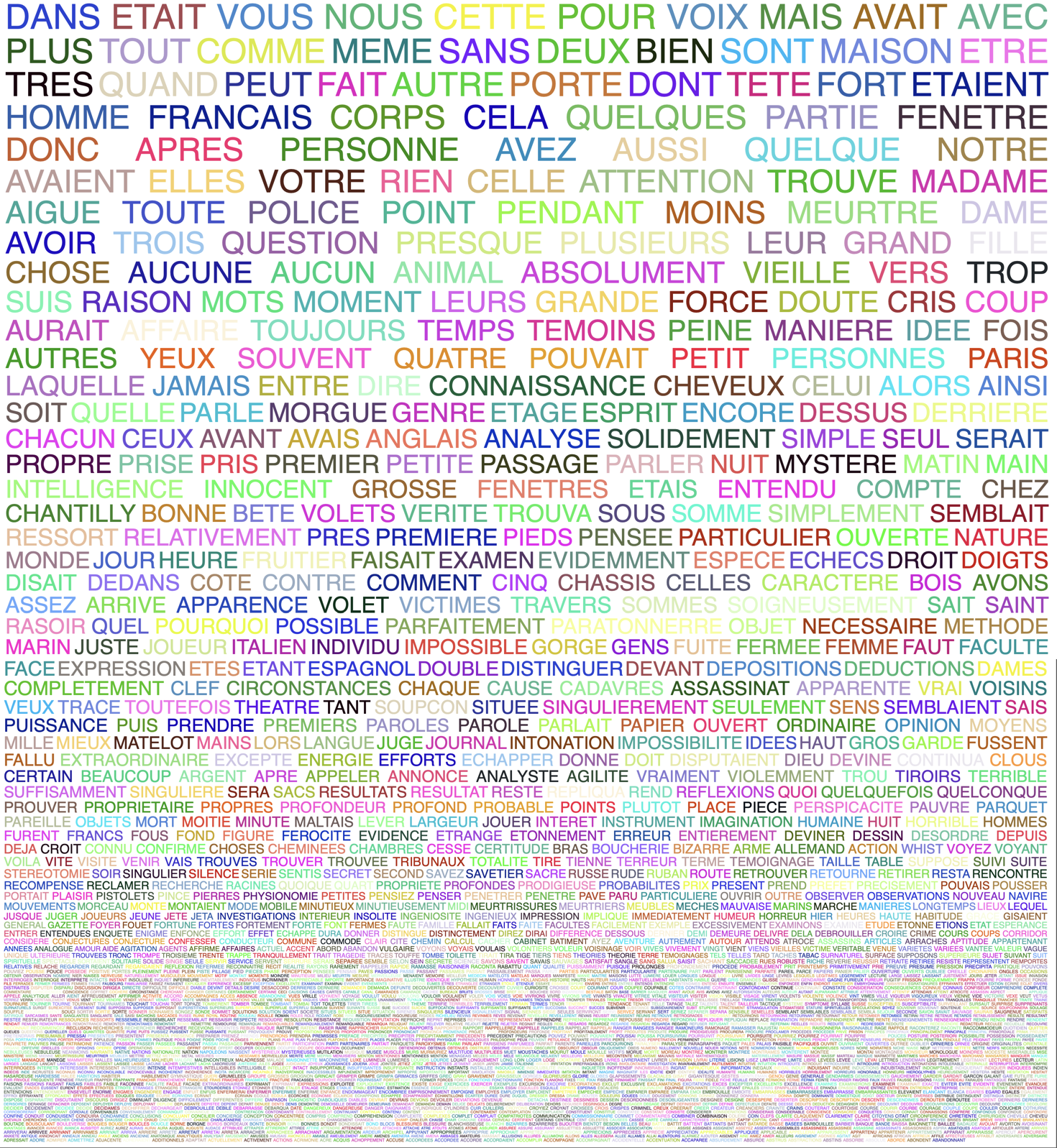
Faust en une page: les nuages de tags sont à la mode et bien connus aujourd’hui, mais le projet présenté à Boris Müller en 2000 a été réalisé avant leurs apparitions: il consistait à faire tenir toute l’œuvre de Goethe, Faust, sur une seule page avec les mots apparaissant en premier selon le nombre décroissant de leurs occurrences.
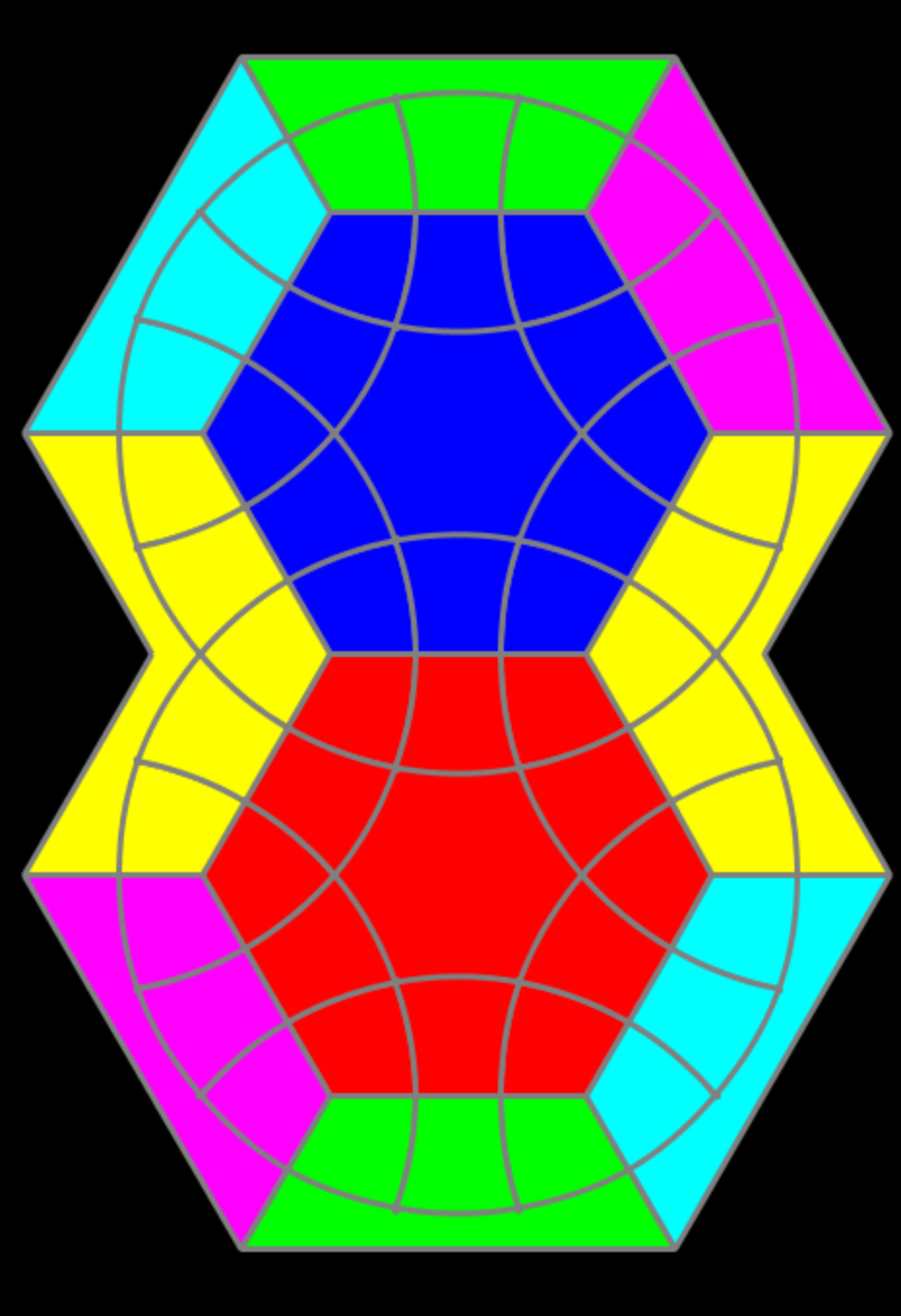
Un démineur original: le jeu du démineur a été popularisé par Microsoft: on le retrouve dans différentes versions de son système d’exploitation. Le jeu de l’hexagone et de la marguerite est probablement son ancêtre. De plus la technique de codage permet de réaliser des mosaïques spectaculaires dont la texture est, une nouvelle fois, fractale.
Un casse-tête pour voyageur de commerce il est parfois étonnant de constater que ce qui peut apparaître comme sérieux est utile également à des domaines plus futiles comme les jeux ou les casse-tête. Ainsi, le code de Gros-Grey utilisé dans le domaine des télécommunications et pour résoudre le problème du voyageur de commerce sur un hyper-cube est utile également pour résoudre le poblème du baguenaudier, des anneaux chinois et un casse-tête plus récent: le «Spin-out».
Lire dans le noir le français Louis Braille, aveugle lui-même, inventa, au début du XIXe siècle, la méthode portant maintenant son nom et permettant aux aveugles du monde entier d’accéder à l’écriture et à la lecture. L’ordinateur a été rapidement associé à la production de documents pour les aveugles.
Découper un puzzle comment fabrique-t-on les pièces? Les formes des pièces de puzzle sont en effet remarquables; elles se ressemblent, tout en étant différentes; lorsqu’elles s’emboîtent, elles ajoutent à la solidité de l’ensemble.
Belles molécules la représentation dans l’espace de molécules est un problème classique faisant appel à l’informatique. L’ordinateur est, en effet, capable de représenter des molécules sous forme de sphères liées entre elles.
La grande illusion l’œuvre d’Escher est fascinante; on y retrouve plusieurs constructions impossibles: Belvédère, Montée et descente, Cascade. Certaines très simples ont inspiré d’autres artistes.
Les lucioles thaïlandaises le monde naturel est rempli d’oscillateurs couplés et les plus remarquables sont ceux des êtres vivants: par exemple, les criquets stridulent à l’unisson et les groupes de lucioles ont une luminescence synchrone. L’ordinateur peut reproduire ce comportement.
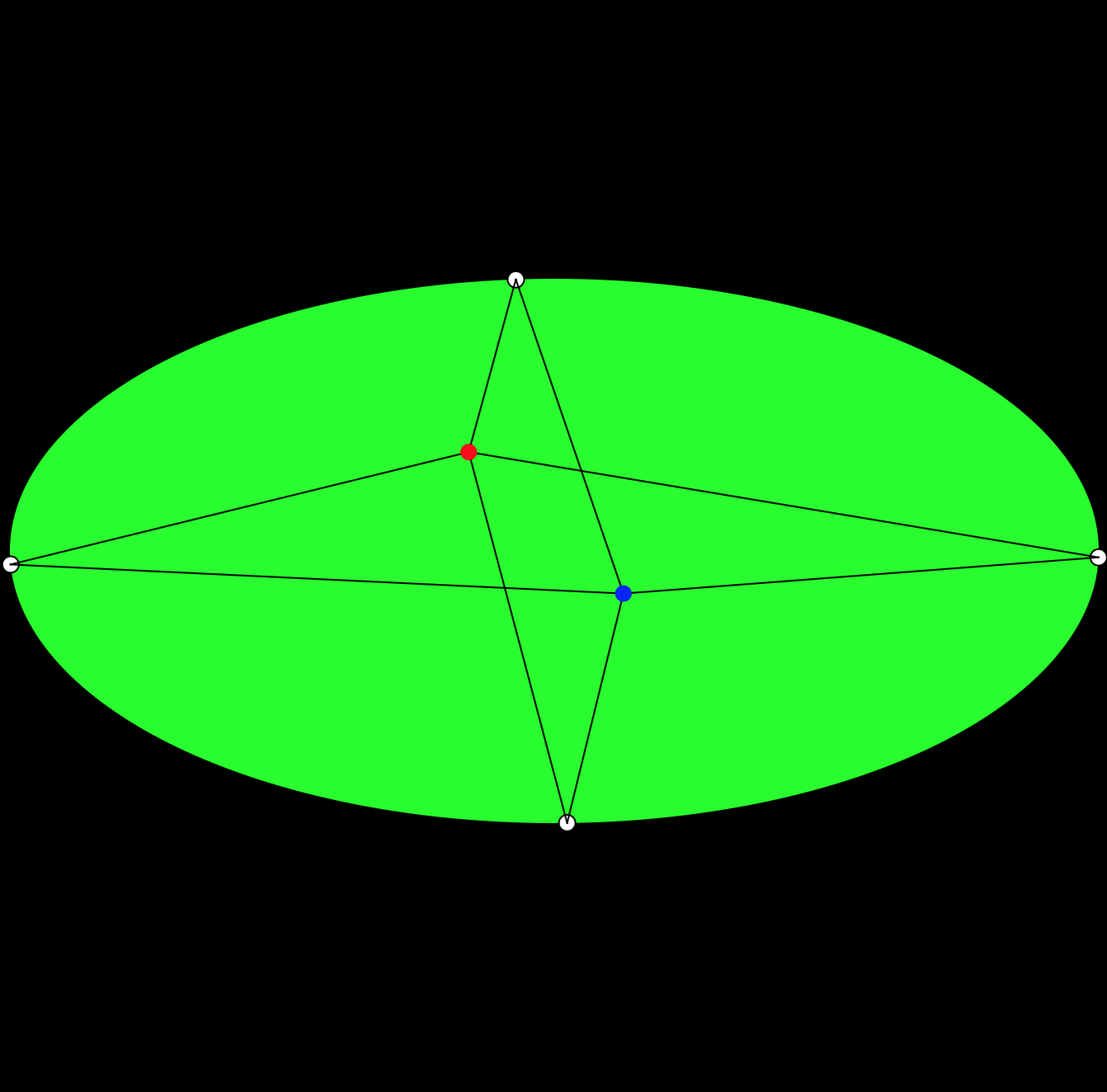
Passer sur un billard l’ordinateur permet de réinventer le jeu de billard en lui donnant des formes exotiques: circulaires, elliptiques, en étoile, etc. La question qui se pose reste toutefois: dans quelle direction tirer une première boule en visant une bande pour atteindre une deuxième balle à coup sûr?
Escher et math Escher a effectué des recherches sur la répétition de motifs pour réaliser une de ses œuvres. L’ordinateur peut reprendre ces réflexions pour les reproduire.
Etrange attracteur Clifford A. Pickover a imaginé une façon originale de mélanger fractals, chaos, graphisme sur ordinateur et science fiction. Suivant les paramètres, une infinité de représentations graphiques originales s’offrent à nous.
Eteindre la lumière Ligths Out est un jeu qui consiste en un tableau contenant 25 lampes/boutons disposés en cinq lignes et cinq colonnes. Au départ certaines lampes sont allumées et d’autres sont éteintes au hasard. Le but du jeu consiste à les éteindre toutes le plus rapidement possible. Les mathématiques peuvent nous aider à résoudre ce problème et même nous donner la solution la plus rapide.
Un trou carré Est-il possible de forer des trous de forme carrée? Franz Reuleaux a donné une solution permettant d’effectuer des forages presque carrés. La figure qu’il a imaginée s’intitule triangles de Reuleaux; elle comporte également d’autres propriétés intéressantes qui permettraient aux fabricants de boutons d’économiser de l’argent.
Le doigt dans l'engrenage les mécanismes horlogers sont constitués essentiellement d’engrenages. Ces derniers sont utilisés pour multiplier ou démultiplier une vitesse d’entrée pour obtenir une vitesse de sortie particulière.
Là haut la ola depuis que la ola mexicaine existe, on peut se demander comment la modéliser. Pourquoi part-elle souvent dans le même sens? Comment la déclencher? Comment la poursuivre ou non? Le but de cet exercice est d’expliquer comment modéliser cette vague de spectateurs que l’on observe de plus en plus dans les stades sportifs.
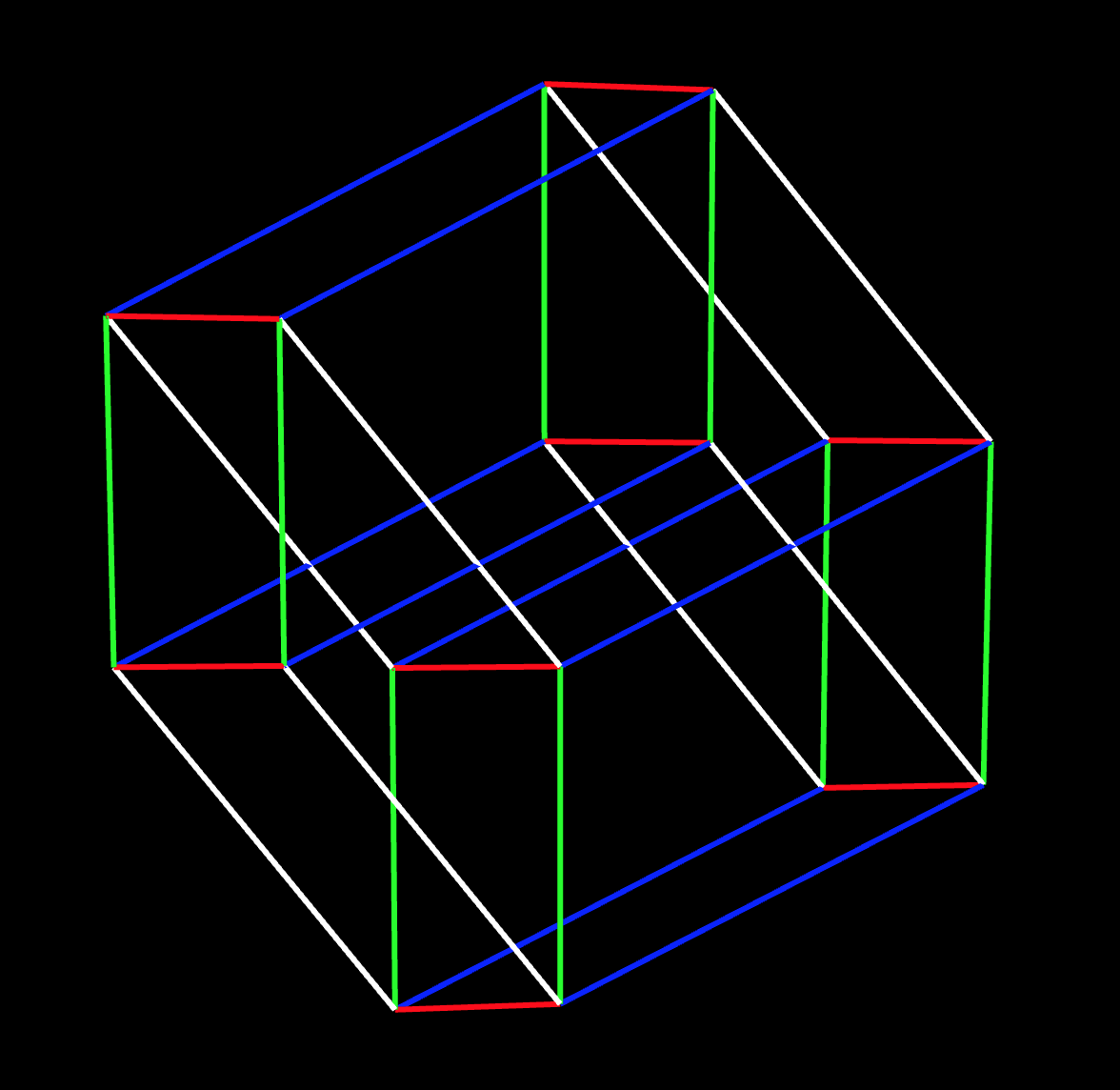
La quatrième dimension quelle serait la réaction d’êtres à deux dimensions si un cube traversait leur monde plan? Il faut commencer à travailler par analogie; à se mettre à la place d’êtres unidimensionnels ou bidimensionnels pour tenter d’imaginer ce qu’est la quatrième dimension. L’ordinateur peut être particulièrement utile en calculant à tout moment la projection d’un objet de dimension supérieure dans une dimension accessible à l’être humain.
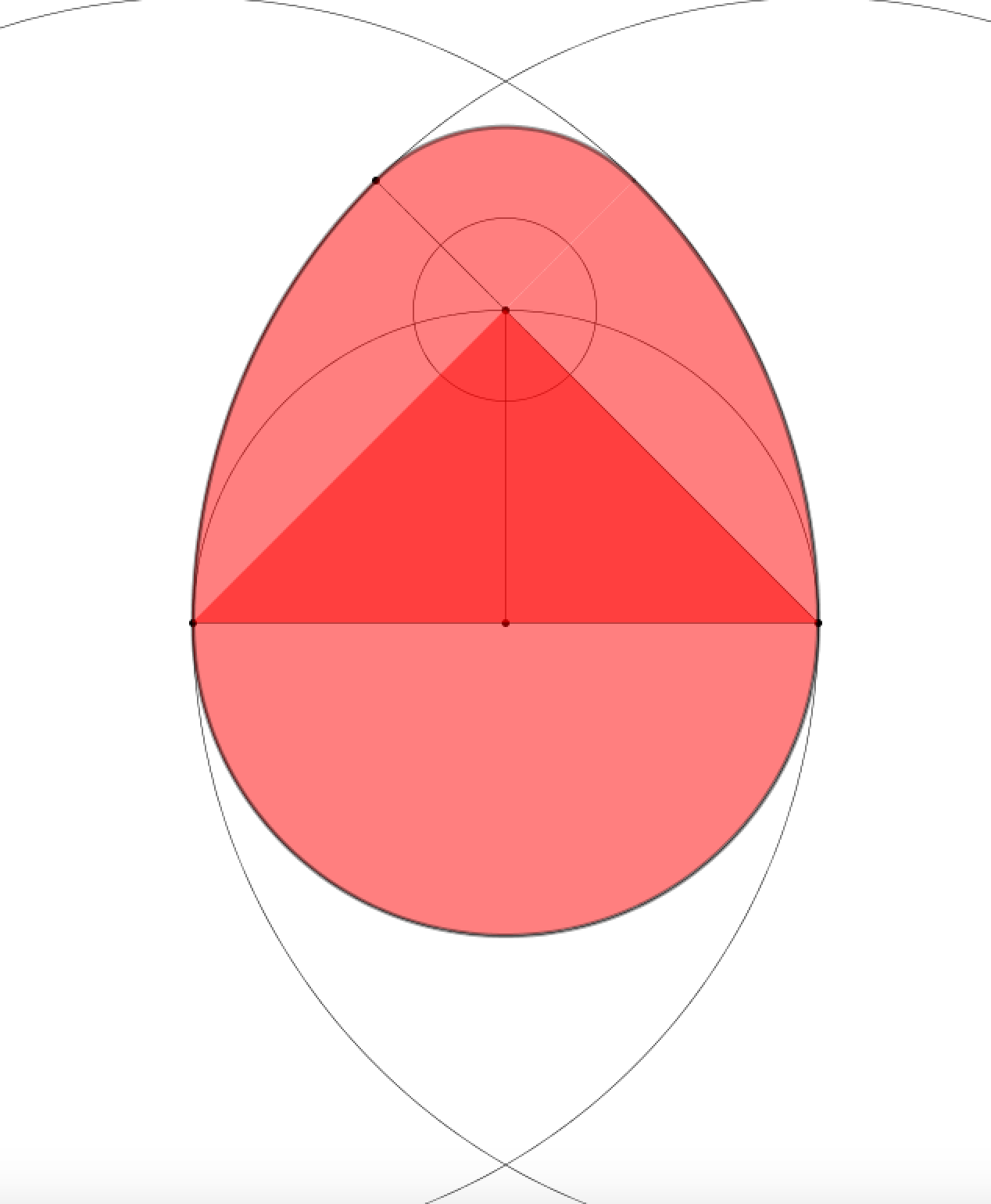
Les œufs de Fabergé Pendant onze années, la tsarine Maria reçut des œufs fabriqués par Fabergé. Les motifs qu’il utilisait étaient symétriques et répétitifs. Aujourd’hui, un informaticien amateur peut réaliser des motifs originaux ressemblant, modestement, aux décors des œufs de Fabergé.
Passerons-nous Pâques aux tisons? La date de Pâques est un condensé du calendrier lunaire-solaire juif et des calendriers julien et grégorien. Les algorithmes permettant de déterminer la date de Pâques sont compliqués et sont truffés de règles spéciales, pour tenir compte des exceptions. En revanche si l’on se limite à la période allant de 1900 à 2099 inclus il existe une méthode très simple conçue par Thomas O’Beirne de Glasgow.
GEB La couverture du livre de Douglas Hofstadter intitulé les Brins d’une Guirlande Eternelle est fascinante à plus d’un titre: la traduction française conserve l’illustration de la version originale anglaise sans trahir le titre. Les lettre B, G et E sont le résultat de projections de face, de dessus et de profil de deux blocs sculptés.
Un calendrier lunaire pour connaître les phases de la lune, quoi de plus parlant qu’un calendrier avec une indication journalière? Mais comment calcule-t-on les phases de la lune? A-t-elle (la lune) un comportement régulier?
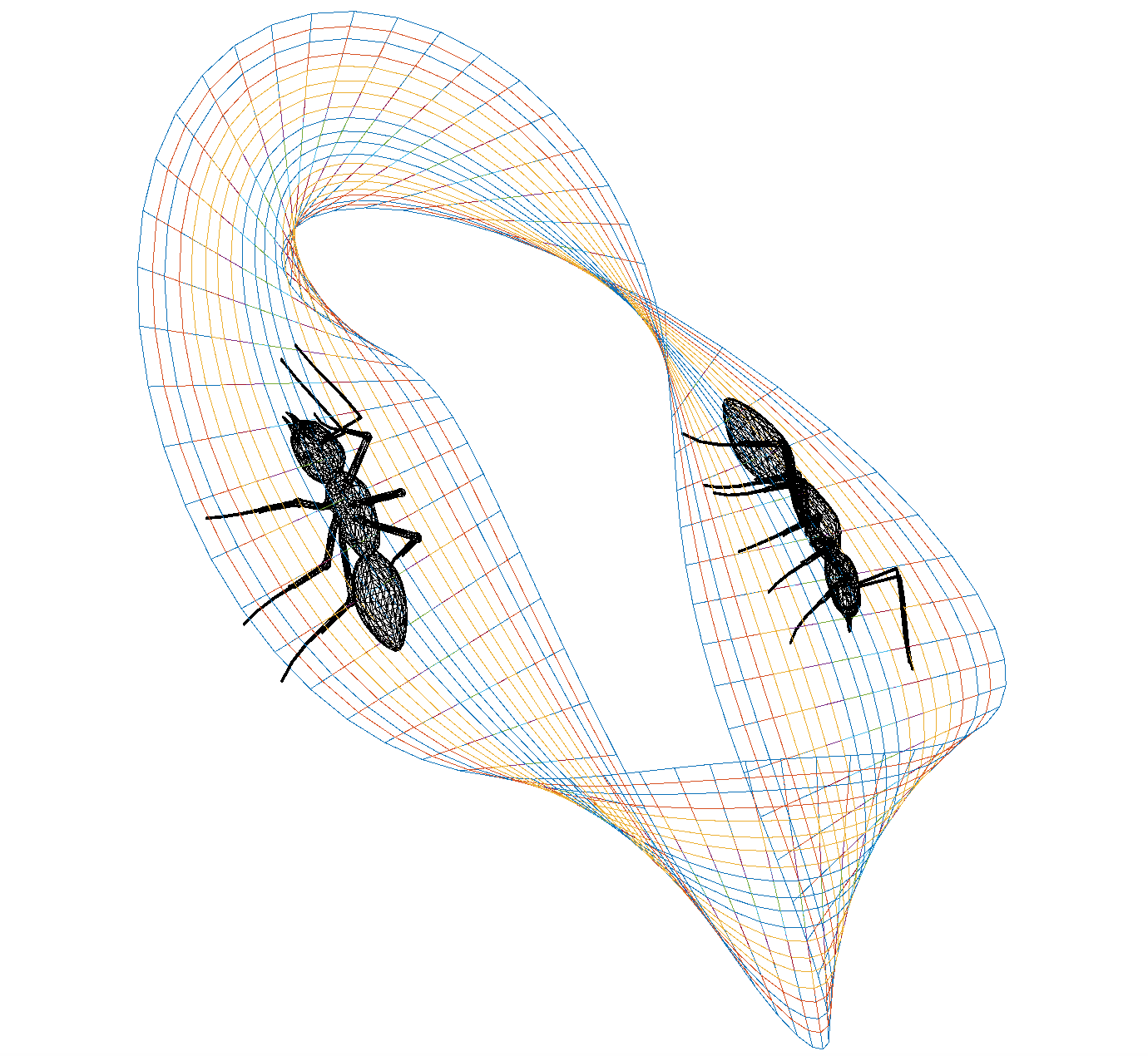
Un ruban à une face et un côté (Moebius) le ruban de Möbius est étrange, car il comporte une face et un seul côté. Cet objet mathématique intéressant en topologie, est facile à construire.
Le jeu de Marienbad le jeu de Marienbad (une forme de jeu de Nim) est très simple. Il se joue à deux joueurs; chacun à son tour enlève d’un tas un certain nombre de jetons; celui qui enlève le dernier a perdu. Ce jeu fait appel à une théorie mathématique des plus inattendues, basée sur la numération binaire.
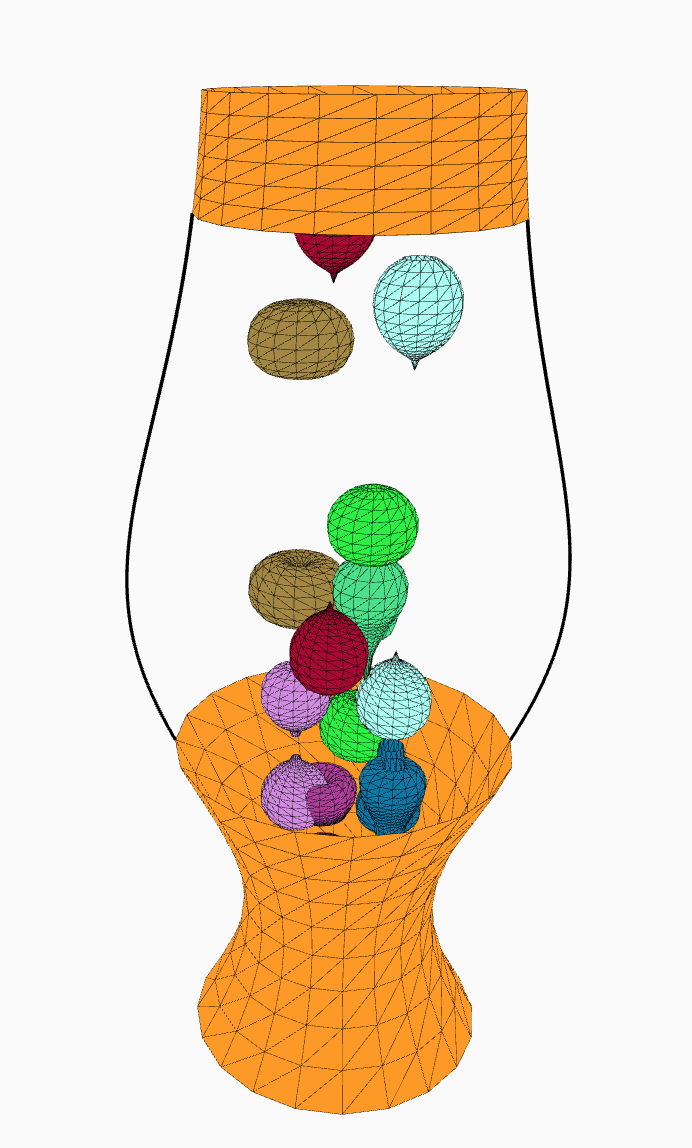
Une lampe, machine à lave une icône culturelle des années 1960 peut renaître sous forme digitale. La lampe de lave est un objet que les mathématiciens peuvent modéliser; dès lors l’objet est virtuel mais, n’est-ce pas un plaisir de pouvoir la décrire entièrement par des formules mathématiques.
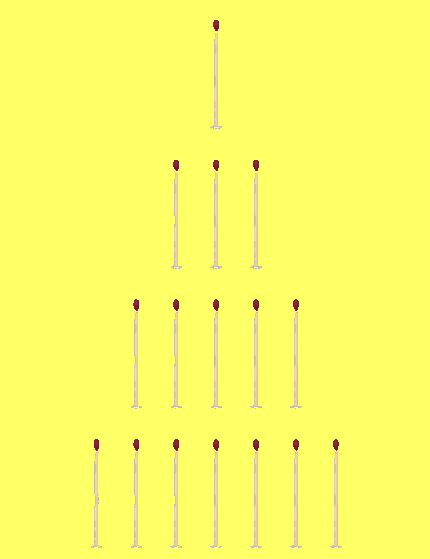
Tout feu tout flamme calculer de façon exacte les dynamiques entourant un système aussi complexe que le feu requiert une simulation poussée. Or une approximation existe permettant de représenter un feu de façon extrêmement réaliste et sans difficulté (si l’on dispose d’un ordinateur). Un exemple d’algorithme simple permettant de modéliser un comportement complexe.
Les anneaux de Borromée ne sont pas reliés deux à deux, et pourtant le groupe ainsi formé est indissociable. Si l’on sectionne l’un des trois anneaux, on obtient trois anneaux séparés.
La formation des cristaux. En partant du hasard on obtient en plusieurs phases successives d’étranges cristallisations qui ressemblent à une forme de vie primitive. Un automate cellulaire, système mathématique très simples à décrire, permet d’observer des images d’une complexité stupéfiante.
Un chercheur de premiers. La recherche des nombres premiers et leur répartition sont des thèmes qui fascinent les mathématiciens et font travailler les ordinateurs. Les représentations graphiques des nombres premiers sont difficiles à imaginer. Toutefois, sur la base des travaux de Stanislaw Marcin Ulam, on peut représenter les nombres de diviseurs des nombres entiers et, ainsi, la répartition des nombres premiers.
La courbe de Hilbert tridimensionnelle. Une extension tridimensionnelle de la courbe de Hilbert, faisant appel à une interprétation sur le modèle de la tortue logo des L-systèmes.
Le baiser infini. La conceptualisation de l’infini pose des problèmes depuis longtemps. Une représentation graphique originale permet d’illustrer ce concept à partir de recherches publiées en 1938 par L. R. Ford: un ensemble de sphères construites à partir des cercles de Ford. Chaque sphère est entourée d’une chaîne infinie de sphères qui l’embrassent.
L'illusion de Shepard: sur le modèle des illusions visuelles, l'illusion de Shepard nous fait croire que les sons continuenet de monter indéfiniment.
Ne jetez pas de pavés à Truchet : à partir d’un même carreau qui peut être tourné au hasard, on obtient un pavage dont les résultats sont spectaculaires. On peut même essayer de colorier chaque trait qui représente un parcours possible dans le pavage. Une version «jeu» est également intéressante : comme au taquin, il y a une case vide dans le pavage; chaque joueur déplace les carreaux verticalement et horizontalement suivant la position de cette case. Le premier qui obtient un chemin qui relie un côté à un autre a gagné.
Géodes & cie : à partir d’un polyèdre régulier, on peut obtenir de multiples versions de géodes, notamment, celle a servi de modèle à la géode de la Villette à Paris.
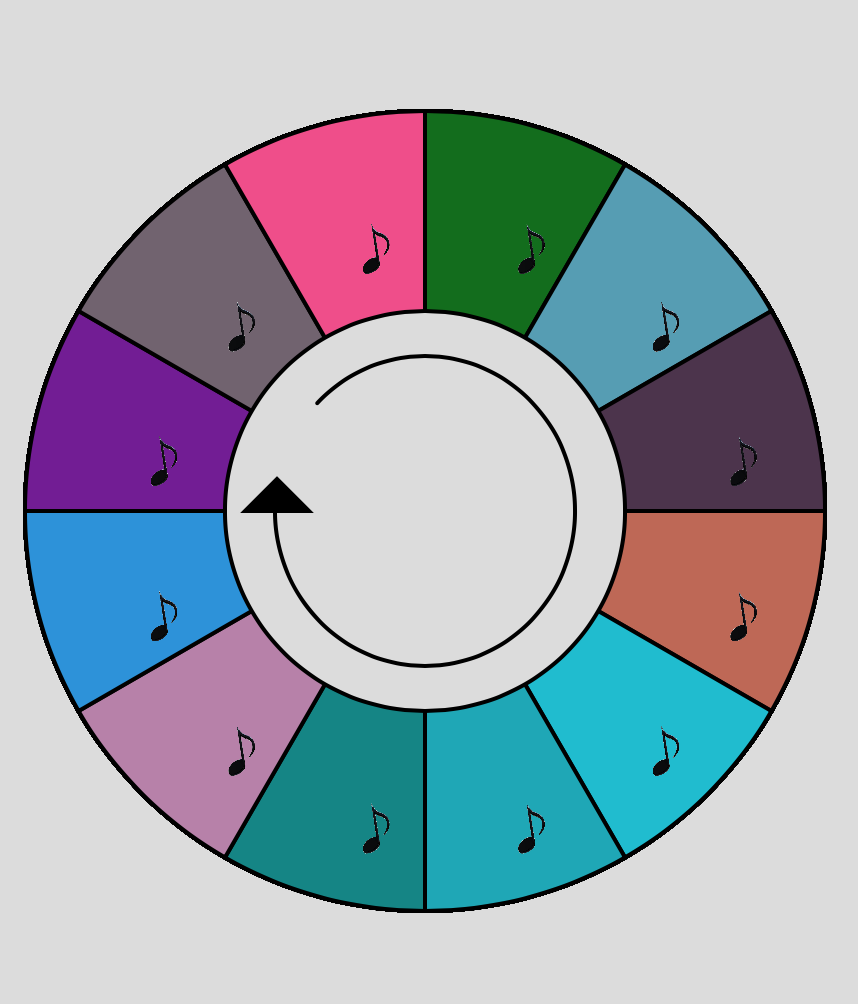
Engel Heart, un casse-tête. Plus difficile qu’un cube Rubik, ce jeu simple à comprendre est difficile à résoudre. En tournant une roue au hasard de 60° à gauche et à droite, on mélange les pièces appelées os et pierres. Le but du jeu consiste à remettre les pièces dans la configuration initiale.
Le cavalier fou: déplacer un cavalier sur toutes les cases d’un échiquier sans repasser sur une case déjà visitée. Un problème à la fois complexe et simple à résoudre pour qui a une bonne mémoire.
Labyrinthe ne fait pas le moine ou les plans de Dédale: comment construire un labyrinthe proche de la perfection? Comment trouver la sortie lorsque l’on s’y est engagé.
Pour qui veut des cartes de vœux ou cartes de vœux fractales: construire une carte de vœu originale en la découpant, pliant et dépliant. Une occupation originale faisant appel aux fractales.
Faire tapisserie: sur le modèle des tapis persans qui font appel aux symétries et aux effets d’auto-similarité, un algorithme peut permettre la représentation à l’infini de tapis virtuels.
ça sent le sapin, un sujet épineux : trouver un algorithme pour représenter un arbre et en particulier un sapin permet de dessiner des sapins virtuels. En période de fêtes, comment l’informatique peut-elle être au service de la décoration?
un tour en vélo: observer la trace d’un point fixe sur une roue de vélo en déplacement peut conduire à des découvertes intéressantes; quelle est le trajet le plus rapide (et non pas le plus court entre deux points sur un plan vertical? Comment glisse une perle le long d’une cycloïde? Comment construire un pendule quasi parfait?
J’aimerais tant voir Syracuse: un problème extrêmement simple mais qui donne lieu à une conjecture que les mathématiciens n’ont pas encore réussi à démontrer.
le cas chaos : représenter l’ensemble de Mandelbrot et d’agrandir des portions de la courbe obtenue. Les choix des couleurs est aléatoire. La résolution peut être modifiée (par défaut: 100 itérations par point), Une applette Java permet de visualiser l’ensemble de Mandelbrot.
en Lissajous, en feu: reproduire un show laser à base de son, simuler un oscilloscope, comparer des fréquences. Les courbes dites de Lissajous sont des modèles mathématiques permettant de comparer les fréquences. Une applette Java permet de visualiser ces courbes en modifiant les fréquences verticales et horizontales ainsi que le déphasage.
Codes-barre ou barbare? que se cache-t-il derrière les mystérieuses petites lignes blanches et noires imprimées sur les étiquettes des produits de consommation, appelées codes-barre? Comment les déchiffrer?
Le suicide des zélotes où faut-il se placer sur un cercle pour être choisi ou pour échapper à un massacre? Ce problème, inspiré d’un fait authentique, est une introduction à la simulation en informatique.
Le dilemme des prisonniers quelle stratégie adopter? Avouer ou trahir, coopérer ou tromper. Le dilemme des prisonniers est devenu un classique, il est un des jeux les plus étudiés pour mieux comprendre la dynamique sociale d’un groupe d’individus en compétition. On peut, avec l’aide d’un ordinateur, expérimenter les avantages respectifs de l’entraide ou de la trahison, sans risquer la prison...
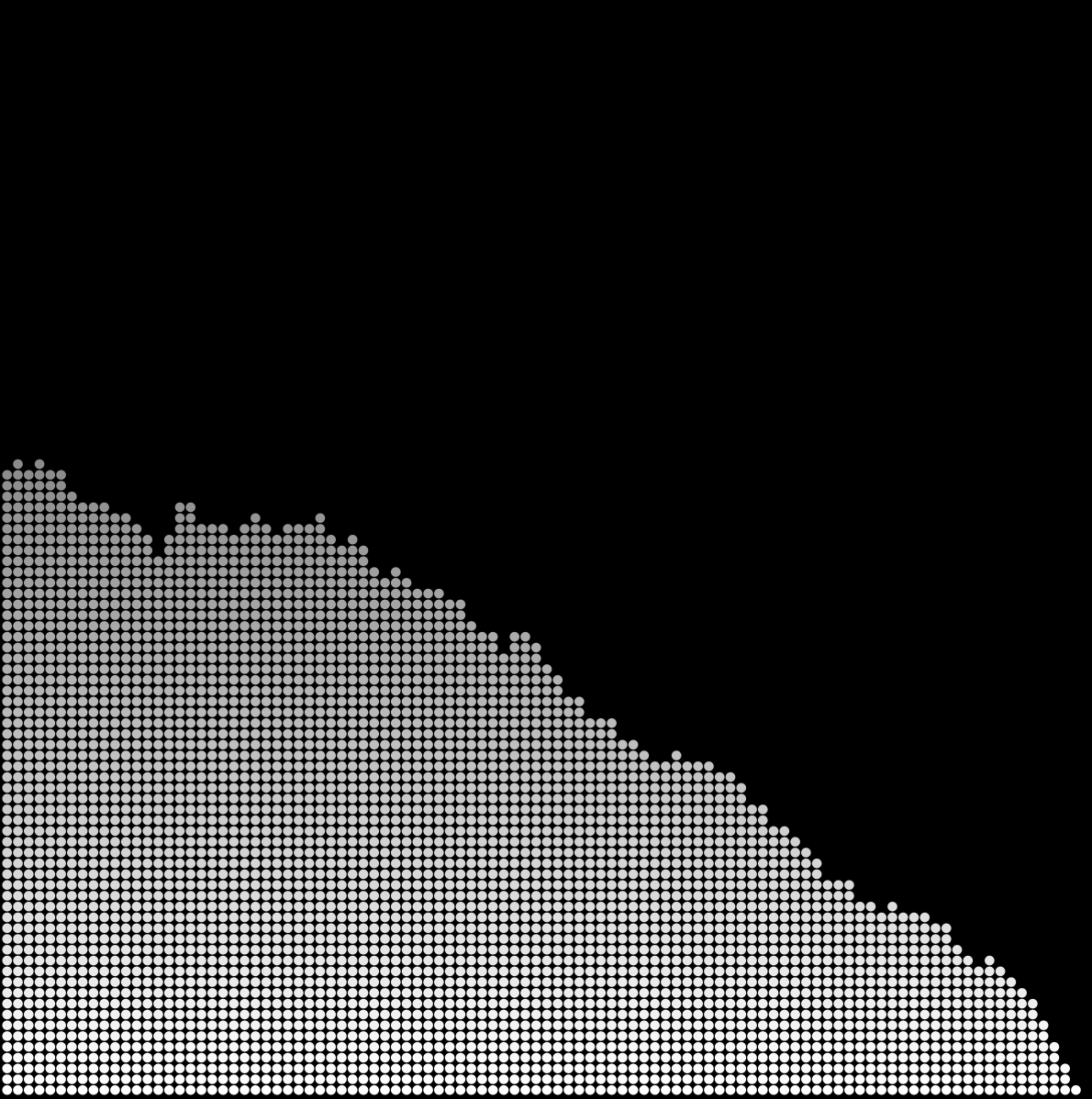
La physique du tas de sable le comportement du sable intéresse beaucoup les physiciens, en particulier le comportement des avalanches. Il est possible, sur un ordinateur, de simuler le comportement de ces avalanches grâce à ce que l’on appelle des automates cellulaires. Le but du problème consiste donc à simuler des avalanches, à calculer leurs tailles et la fréquence en fonction du temps.
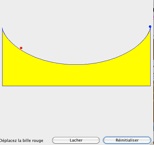
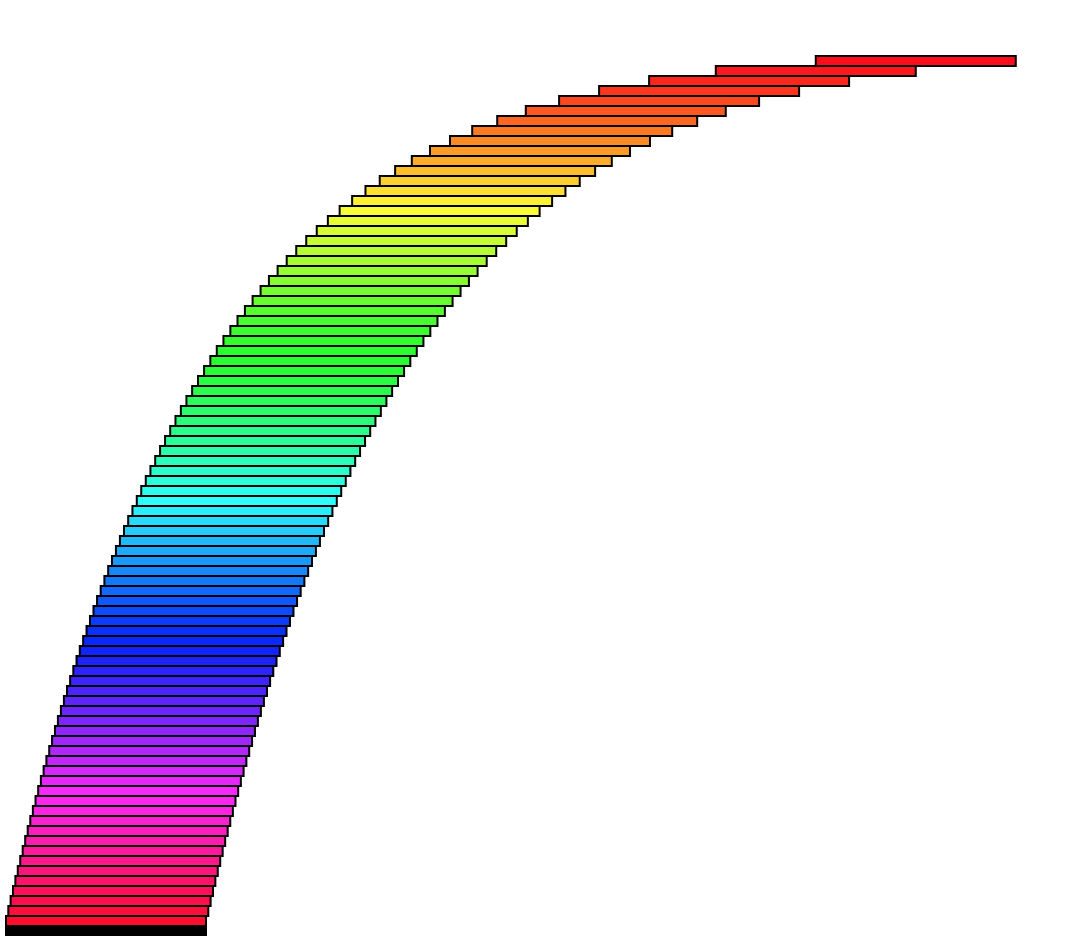
Une tour de cartes On dispose de beaucoup de cartes. A quelle distance maximale du bord de la table se trouvera la dernière carte, en faisant en sorte que les cartes restent en équilibre sur celle-ci?
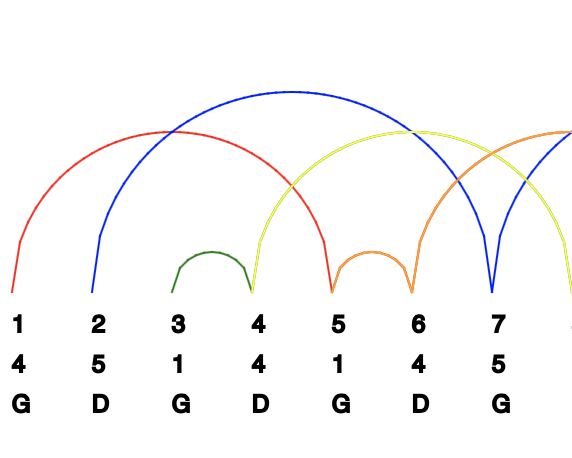
Numéros de jonglerie Comment les jongleurs parviennent-ils à lancer et à rattraper balles et anneaux avec tant d’adresse? L’étude de leur activité est utile en psychomotricité, en robotique et en mathématiques. Une des méthodes utilisées est la notation d’échange de position qui représente l’ordre dans lequel les objets sont lancés et rattrapés dans chaque cycle de jonglerie.
Poster un commentaire de mathématicien Aristote, le plus grand de tous les philosophes, méritait bien qu’on le commente, ce que fit Averoes (parmi bien d’autres) au XIIe siècle. Saint Thomas d’Aquin commenta ce commentaire (qu’il désapprouvait) et il fut lui-même commenté par Etienne Gilson qui lui-même... Que dire alors du commentaire mathématique? On peut aborder cette question par un casse-tête, puis on peut prolonger la réflexion sur les structures mathématiques.
Hercule et son clebs hydre Hercule doit accomplir douze travaux. Parmi ceux-ci, il doit couper les têtes d’une hydre; celles-ci repoussent constamment. En supposant qu’Hercule soit immortel, aura-t-il suffisamment de temps pour les couper toutes? Le problème est intéressant mathématiquement du point de vue de la théorie des nombres. La réponse est surprenante et, avec un ordinateur, on peut pousser la simulation très loin.
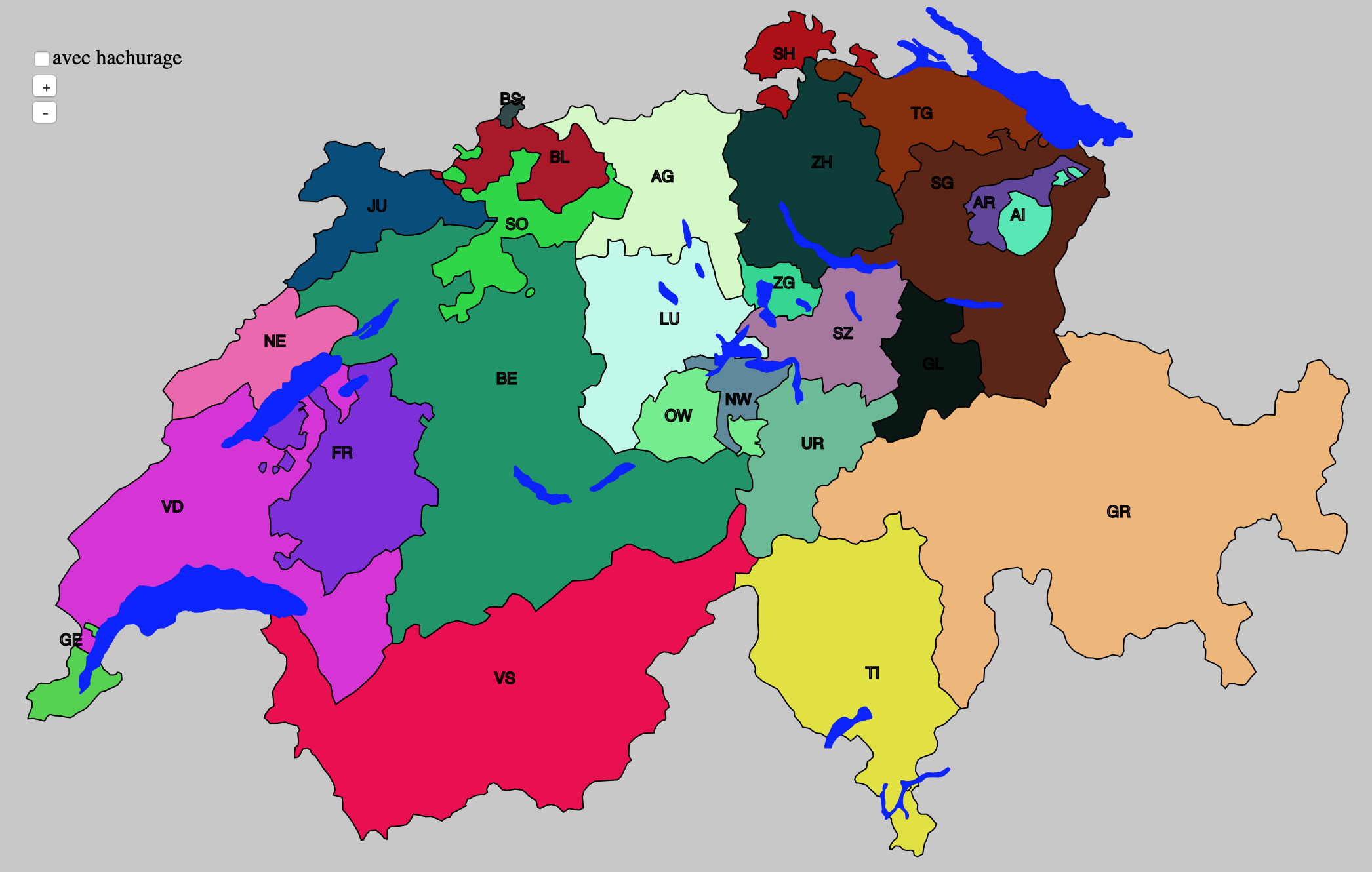
Hachurer la Suisse pour représenter les différences entre cantons, on utilise souvent des représentations construites sur la carte de la Suisse en coloriant et/ou hachurant les cantons en fonction de critères précis.
Panem et circenses: comment dessiner un amphithéâtre sur le modèle du Colisée.