Résumé: une icône culturelle des années 1960 peut renaître sous forme digitale. La lampe de lave est un objet que les mathématiciens peuvent modéliser; dès lors l’objet est virtuel mais, n’est-ce pas un plaisir de pouvoir la décrire entièrement par des formules mathématiques.
Mots-clés: cylindre, sphère, polynôme de Legendre, transformation, simulation, lampe, lave.
Solution:
La solution actuellement proposée est donnée en P5JS.

thèmes
de plus
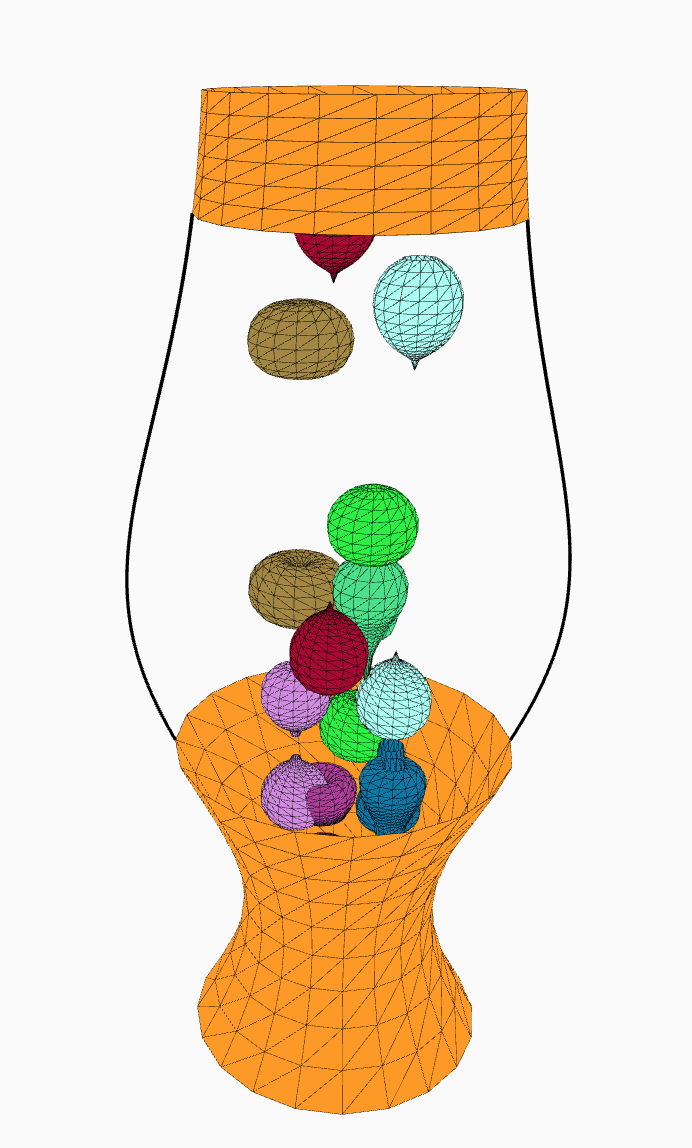
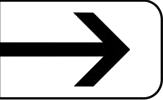
Une lampe à lave
L’exercice s’inspire de la revue The Mathematica Journal, Lava Lamp, de Robert Rudd, Miller Freeman Publication, 1995.
L’anglais, Craven Walker, est la personne responsable de la prolifération des lampes à lave dans le monde. L’identité de l’inventeur est controversée: certains soutiennent que Craven Walker fut l’inventeur (il travaillait sur un timer pour préparer les œufs); d’autres affirment qu’il s’agirait d’un certain Mr. Dunnett.
Dans tous les cas, Craven Walker travailla plus de 15 ans pour perfectionner son mélange et vendit sa lampe en fondant son entreprise Crestworth Company. Plus tard Crestworth devint Mathmos, le teneur de la patente européenne.
En 1965, deux hommes de Chicago, Adolph Wertheimer et Hy Spector, virent la lampe de Craven lors d’une foire en Allemagne et achetèrent les droits. L’entreprise américaine prit le nom de Lava-Simplex Inc.
Craven jouit maintenant de sa popularité puisque la nouvelle génération semble s’y intéresser à nouveau (après la grande dépression de la lampe à lave dans les années 1980). Il déclare aux personnes qui n’apprécient pas sa lampe qu’elles sont effrayées par... le sexe.
Mais, comment fonctionne une lampe à lave? Un récipient rempli de liquide transparent contient une substance non soluble dans l’eau (la lave) qui est légèrement plus dense (plus lourd) et qui bénéficie d’un coefficient d’expansion thermique important. Ainsi, il reste au fond du récipient. Une source de chaleur au fond du récipient réchauffe la substance, en faisant augmenter le volume et en devenant moins dense que le liquide qui l’entoure. Ainsi, il s’éloigne de la source de chaleur, se refroidit, se contracte légèrement et devient (à nouveau) plus dense. Il tombe. Lourd, léger, lourd, léger. Dense, moins dense, dense, moins dense.
Les recettes pour fabriquer ces lampes restent secrètes. On en trouve toutefois sur Internet. Pour la lave on utilise généralement de l’huile minérale ; pour l’autre liquide on mélange de l’alcool isopropylique à 90% et de l’alcool isopropylique à 70%.
Le but du problème est de simuler le fonctionnement de cette lampe de lave à l’aide d’un ordinateur.
Indications
Le problème exige beaucoup d’expérimentations pour déterminer les paramètres corrects permettant de représenter une lampe de lave. Dans le journal Mathematica, toutes les précisions sont données. Nous les prendrons telles quelles.
La lampe elle-même est constituée par un cylindre dont le rayon est donné par l’expression:
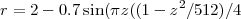
Les quatres parties sont le bas, le haut, le couvercle et la partie transparente centrale.
Chaque lave démarre avec une sphère approximative. Elle se déforme suivant la verticale jusqu’à ce qu’elle se sépare en deux parties. Le temps critique de la séparation est tc = 0.25 (la durée d’une montée est d’une seconde).
Chaque lave est constituée de deux moitiés qui partagent un bord commun. Une sphère est donnée par les coordonnées sphériques suivantes:
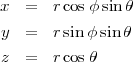
Attention, les nombres viennent vite très grands. Pour éviter d’allonger les temps de calcul, il faut user d’astuce (par exemple, simplifier lorsque les hydres n’ont qu’une seule tête).
Le rayon est l’expression la plus complexe à définir. Robert Rudd choisit le rayon initial suivant:
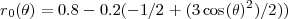
(en réalité, il s’agit d’un polynôme de Legendre).
Le rayon est constant jusqu’au temps critique et devient une sinusoïde corrigée par une exponentielle après:
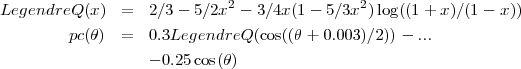
La dépendance au temps est donnée par:
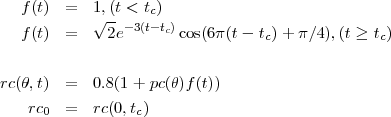
Comme les deux morceaux de lave partagent un bord commun jusqu’au temps critique, ils doivent être déplacés verticalement. La distance verticale est constante jusqu’au temps critique et décroit exponentiellement après le temps critique:
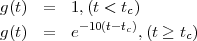
Les formes de lave au temps 0 et dépendant du temps sont:
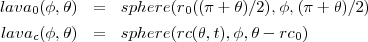
Une fonction effectue la transformation d’une fonction en une autre (paramétrée par une fonction gaussienne du temps):
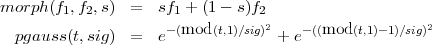
La formule pour une demi-lave est:

Pour obtenir une impression continue, on prendra pour θ la fonction suivante:
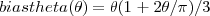
La partie supérieure se déplace vers le haut de façon sinusoïdale. La part inférieure suit la partie supérieure jusqu’au temps critique puis, coule vers le fond:
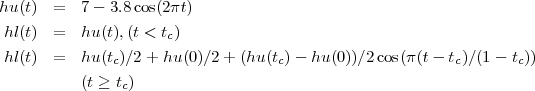
Version P5.JS. Instructions: rechargez la page pour avoir d'autres couleurs pour les laves.