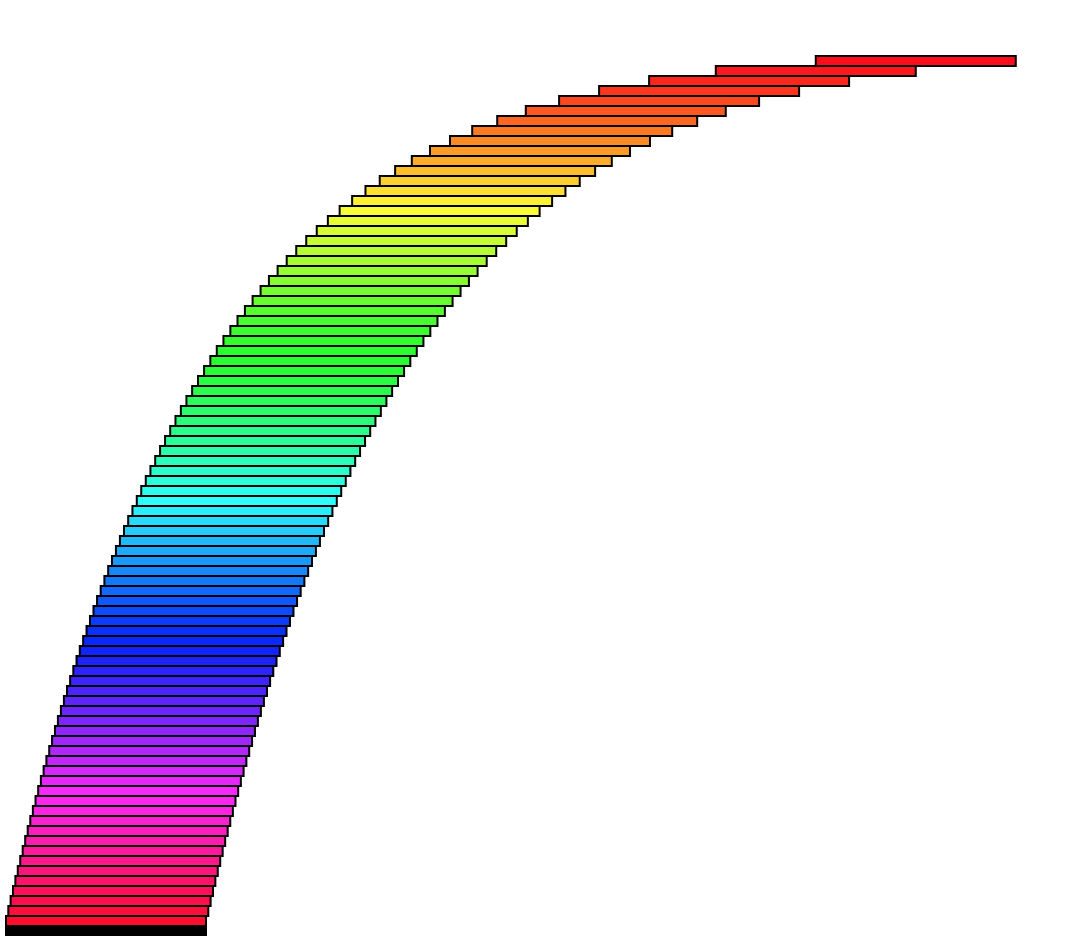
Résumé: on dispose de beaucoup de cartes. A quelle distance maximale du bord de la table se trouvera la dernière carte, en faisant en sorte que les cartes restent en équilibre sur celle-ci?
Mots-clés: théorie des nombres, grand nombre, constante d’Euler, intégration, série, approximation, calcul d’erreurs, cartes.
Solution:
La solution actuellement proposée est donnée en P5JS.

thèmes
de plus
Une tour de cartes
Soient n cartes à jouer et une table, on souhaite construire un surplomb le plus large possible en empilant les cartes sur le bord de la table, en tenant compte des lois de la gravitation selon le modèle suivant
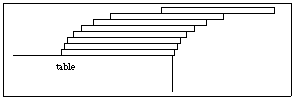
On peut préciser un peu plus le problème en indiquant que les bords des cartes sont parallèles aux bords de la table et que les cartes ont une longueur de 2 unités. Avec une carte, on obtient le surplomb le plus grand lorsque son centre de gravité est au milieu de la carte, ainsi on a un surplomb d’une unité.
Quel est le surplomb maximum si l’on place de façon idéale 52 cartes sur le bord de la table?
Un autre problème amusant ressemble à celui-ci : le ver sur un élastique. Un ver lent mais opiniâtre, V , prend le départ à une extrêmité d’un élastique d’un mètre de long et rampe à la vitesse d’un centimètre par minute vers l’autre extrêmité. A chaque minute, un gardien également opiniâtre, G, dont le seul but est de frustrer V , étire l’élastique d’un mètre. Ainsi après une minute passée à ramper, V est à 1 centimètre du départ et à 99 de l’arrivée ; puis G étire l’élastique d’un mètre. Pendant cette opération, V conserve sa position relative, 1% du départ et 99% de l’arrivée; ou encore, V est maintenant à 2cm du point de départ et à 198cm de l’objectif. Est-ce que le ver atteindra le bout? On suppose que V et G ont une longévité infinie, l’élastique, une élasticité infinie et que le ver soit infiniment mince.
Cet exercice est tiré du livre Concrete Mathematics de Graham, Knuth et Patashnik publié chez Addison Wesley, 1989.
Indications
Calculez la distance entre la table et le bord de la carte en fonction de la carte précédente. Construisez une formule de récurrence pour la calculer en fonction de n cartes. Démontrez-la par induction.
Pour définir le problème un peu plus précisément, il faut imposer que les bords des cartes soient parallèles au bord de la table. Sinon, on pourrait augmenter le surplomb en faisant tourner les cartes les unes au-dessus des autres. Pour simplifier, on considère qu’une carte à une longueur de 2 unités.
Avec une carte, le surplomb maximum est atteint lorsque le centre de gravité de la carte est placé exactement au-dessus du bord de la table. Le centre de gravité est situé au milieu de la carte, ainsi on obtient un surplomb d’une demi-carte de longueur 1 unité. Avec deux cartes il est facile de se convaincre que le surplomb maximum est atteint lorsque le centre de gravité de la carte du haut est situé au-dessus du bord de la carte du bas et que le centre de gravité des deux cartes ainsi disposées est placé au-dessus du bord de la table. Ce dernier est placé au milieu de leur partie commune ; on peut donc ajouter un surplomb d’une demi-unité. Cette façon de placer les cartes suggère une méthode générale, dans laquelle on dispose les cartes de telle sorte que le centre de gravité des k cartes du dessus se trouve juste au-dessus de la k + 1e. La table joue le rôle de la n + 1e carte. Si l’on appelle dk la distance entre le bord extrême de la carte du haut et le bord de la ke carte, alors d1 = 0 et dk+1 doit indiquer le centre de gravité des k cartes :
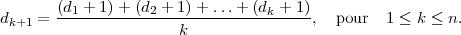
Le centre de gravité de k objets ayant pour poids respectifs, w1,…,wk et ayant leurs centres de gravité respectifs aux positions p1,…,pk se trouve à la position (w1p1 + … + wkpk)∕(w1 + … + wk).
On peut écrire la formule ci-dessus sous la forme équivalente:
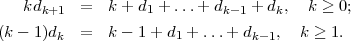
En soustrayant les deux équations, on obtient:
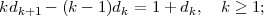
et donc dk+1 = dk + 1∕k. La deuxième carte aura un surplomb d’une demi-unité de plus que la troisième qui a un surplomb d’un tiers d’unité de plus que la quatrième et ainsi de suite. La formule générale est donc:
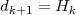
où Hk est communément appelée la série harmonique:
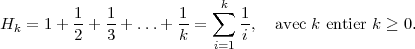
On peut remarquer qu’il ne faut pas beaucoup de cartes pour que celle du haut dépasse la table de toute sa longueur. Le premier nombre Hk qui dépasse 2 (la longueur de la carte) est H4 = 25/12, il suffit donc de quatre cartes.
Avec 52 cartes on a un surplomb de H52∕2 qui donne approximativement 2,27 longueurs de carte.
Pour le problème du ver, il est conseillé d’utiliser les résultats du calcul intégral (et l’approximation par les rectangles) pour calculer de très grands nombres. Des formules plus précises peuvent également être empruntées aux ouvrages de mathématique.
Version p5.js. Instructions: déplacez le curseur pour changer le nombre de cartes et cliquez sur le bouton pour déplacer une carte après l'autre.