Résumé : le pavage consiste à remplir une surface d’un motif particulier. Le pavage de Truchet est très simple et remplit les surfaces de façon très agréable. La représentation du pavage se complique si l’on désire tracer les courbes dans la même couleur.
Mots-clés : symétrie, pavage, parité, cristaux, géométrie, polygone.
Solutions :
La solution actuellement proposée est donnée en P5JS.
Liens : Jeux et Mathématiques

thèmes
de plus
Sous les pavés, Truchet.
L’exercice s’inspire d’un concours organisé par l’association GUTenberg. Le problème a été retrouvé, proposé et initialement étudié par Philippe Esperet, professeur de mathématiques au Lycée Henri IV, Paris, 1995.
« En 1704, le prêtre dominicain Sébastien Truchet, qui s’intéressait aussi aux mathématiques et aux arts, a publié un texte où il montrait qu’une infinité de motifs peuvent être générés par l’assemblage de carreaux coloriés par moitié. Dans ce texte figurait en fait une toute première expression des principes de la théorie combinatoire et de la symétrie cristalline. De plus, ce texte de Truchet a été à l’origine d’un travail d’un autre dominicain du nom de Douat, qui a publié en 1722 un livre contenant une grande quantité de dessins juxtaposant des motifs de base. Ce livre a eu une influence sur tout l’art décoratif européen du 18e siècle. » (d’après Cyril S. Smith, The Tiling Patterns of Sebastien Truchet ant the Topology of Structural Hierarchy, Leonardo, Volume 20, Numéro 4, 1987, pages 373-385).
Le principe est très simple : on dispose d’un nombre illimité de carreaux du type indiqué. En déterminant au hasard leur rotation (il n’y a en fait que deux positions possibles), on pave le plan en assemblant ceux-ci.
Le problème peut se décomposer en trois parties :
-
•tracé des courbes elles-mêmes (selon un procédé aléatoire) ;
-
•coloration des lignes ;
-
•coloration des surfaces délimitées par les différentes courbes fermées et les bords du cadre.
En assemblant les carreaux, on obtient donc de très belles surfaces comme celle-ci :

ou encore

On retrouve le même type de problème dans Curiosités géométriques par Emile Fourrey, Vuibert, Paris, 1907. Il s’agit de recouvrir un plan au moyen de polygones réguliers convexes, sans vides, duplicatures et empiètements. On peut alors considérer deux type d’assemblages : des assemblages de polygones réguliers de même type ou des assemblages de polygones réguliers de types différents. La solution du premier cas a été donnée par les Pythagoriciens. L’étude du second cas a été ébauchée dans l’immortel ouvrage de Kepler, L’Harmonique du Monde, 1619.
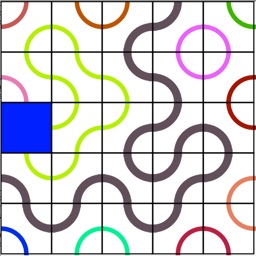
Un jeu a été imaginé à partir du pavage de Truchet: on prend un pavage de 5x5 avec un carreau vide comme ci-dessous. Chaque joueur déplace les carreaux verticalement ou horizontalement en tenant compte de cette case, comme dans le jeu du taquin. Le premier joueur ayant réussi à composer un chemin qui relie un côté à un autre a gagné. Le début de partie se présente ainsi:

La fin de partie peut se présenter ainsi (le chemin solution est plus épais):
Indications
Comme d’habitude, il est conseillé de commencer par ce qui est facile : définir un pavage de Truchet en noir et blanc. Il suffit donc de construire les deux types de carreaux à partir d’arcs de cercles. Pour l’assemblage, on définit une matrice de nombres aléatoires (0 ou 1). Les valeurs indiquent le type de carreau à prendre. Pour la coloration des surfaces à l’aide de deux couleurs seulement, il est conseillé d’observer la parité des lignes et des colonnes.
Pour la coloration des courbes, il est conseillé de considérer tous les cas possibles (cases au bord, dans des lignes paires ou impaires, etc.). Une autre méthode, plus simple, consiste à se déplacer le long de la courbe.
Pour les assemblages de polygones réguliers de type différents, on peut prouver que :
-
•on ne peut avoir autour d’un point plus de 6 polygones convexes ;
-
•on ne peut placer moins de 3 polygones réguliers (donc assemblages ternaires, quaternaires, quinaires et senaires) ;
-
•les angles au centre des centres des polygones sont également les angles au centre des polygones réguliers concernés (donc lorsque les assemblages sont ternaires, quaternaires, quinaire ou senaire, le polygone des centres sera un triangle, un quadrilatère, un pentagone ou un hexagone).
Version P5JS. Instructions: C change la couleur, T affiche les traits et B affiche les chemins colorés.